
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Với \(x\ge\dfrac{1}{6}\Leftrightarrow A=5x^2-6x+1-1=5x^2-6x\)
\(A=5\left(x^2-2\cdot\dfrac{3}{5}x+\dfrac{9}{25}\right)-\dfrac{9}{5}=5\left(x-\dfrac{3}{5}\right)^2-\dfrac{9}{5}\ge-\dfrac{9}{5}\\ A_{min}=-\dfrac{9}{5}\Leftrightarrow x=\dfrac{3}{5}\left(1\right)\)
Với \(x< \dfrac{1}{6}\Leftrightarrow A=5x^2+6x-1-1=5x^2+6x-2\)
\(A=5\left(x^2+2\cdot\dfrac{3}{5}x+\dfrac{9}{25}\right)-\dfrac{19}{5}=5\left(x+\dfrac{3}{5}\right)^2-\dfrac{19}{5}\ge-\dfrac{19}{5}\\ A_{min}=-\dfrac{19}{5}\Leftrightarrow x=-\dfrac{3}{5}\left(2\right)\\ \left(1\right)\left(2\right)\Leftrightarrow A_{min}=-\dfrac{19}{5}\Leftrightarrow x=-\dfrac{3}{5}\)
Với \(x\ge\dfrac{1}{3}\Leftrightarrow B=9x^2-6x-4\left(3x-1\right)+6=9x^2-18x+10\)
\(B=9\left(x^2-2x+1\right)+1=9\left(x-1\right)^2+1\ge1\\ B_{min}=1\Leftrightarrow x=1\left(1\right)\)
Với \(x< \dfrac{1}{3}\Leftrightarrow B=9x^2-6x+4\left(3x-1\right)+6=9x^2+6x+2\)
\(B=\left(9x^2+6x+1\right)+1=\left(3x+1\right)^2+1\ge1\\ B_{min}=1\Leftrightarrow x=-\dfrac{1}{3}\left(2\right)\)
\(\left(1\right)\left(2\right)\Leftrightarrow B_{min}=1\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{3}\end{matrix}\right.\)

`M=-9x^2+6x-3`
`M=-(9x^2-6x+3)`
`M=-(9x^2-6x+1+2)`
`M=-(3x-1)^2-2`
Vì `-(3x-1)^2 <= 0 AA x`
`<=>-(3x-1)^2-2 <= -2 AA x`
Hay `M <= -2 AA x`
Dấu "`=`" xảy ra `<=>(3x-1)^2=0<=>3x-1=0<=>x=1/3`
Vậy `GTLN` của `M` là `-2` khi `x=1/3`
\(M=-9x^2+6x-3\)
\(M=-\left(9x^2-6x+3\right)\)
\(M=-\left[\left(3x-1\right)^2+2\right]\)
\(M=-\left(3x-1\right)^2-2\)
\(\Rightarrow Max_M=-2\) khi \(3x-1=0\)
\(\Leftrightarrow x=\dfrac{1}{3}\)

\(=\left(9x^2-6x+1\right)+4=\left(3x-1\right)^2+4\ge4\)
Dấu \("="\Leftrightarrow x=\dfrac{1}{3}\)

1/
a, \(A=4x^2-4x+5=4x^2-4x+1+4=\left(2x-1\right)^2+4\ge4\)
Dấu "=" xảy ra khi x=1/2
Vậy Amin=4 khi x=1/2
b, \(B=3x^2+6x-1=3\left(x^2+2x+1\right)-4=3\left(x+1\right)^2-4\ge-4\)
Dấu "=" xảy ra khi x=-1
Vậy Bmin = -4 khi x=-1
2/
a, \(A=10+6x-x^2=-\left(x^2-6x+9\right)+19=-\left(x-3\right)^2+19\le19\)
Dấu "=" xảy ra khi x=3
Vậy Amax = 19 khi x=3
b, \(B=7-5x-2x^2=-2\left(x^2-\frac{5}{2}x+\frac{25}{16}\right)+\frac{31}{8}=-2\left(x-\frac{5}{4}\right)^2+\frac{31}{8}\le\frac{31}{8}\)
Dấu "=" xảy ra khi x=5/4
Vậy Bmax = 31/8 khi x=5/4
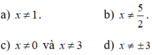

`2/[6x-5-9x^2]`
`=-2/[9x^2-6x+5]`
`=-2/[(3x-1)^2+4]`
Vì `(3x-1)^2 >= 0 AA x`
`<=>(3x-1)^2+4 >= 4 AA x`
`<=>1/[(3x-1)^2+4] <= 1/4`
`<=>-2/[(3x-1)^2+4] >= -1/2 AA x`
`=>Mi n=-1/2`
Dấu "`=`" xảy ra `<=>3x-1=0<=>x=1/3`