A
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
12 tháng 2 2017
Đáp án đúng : C
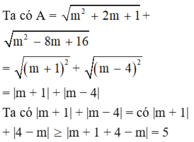
Dấu “=” xảy ra ⇔ m + 1 4 − m ≥ 0
⇔ − 1 ≤ m ≤ 4
Vậy GTNN của A là 5 khi − 1 ≤ m ≤ 4
TV
1
30 tháng 12 2023
\(A=\sqrt{m^2+2m+1}+\sqrt{m^2-8m+16}\)
\(=\sqrt{\left(m+1\right)^2}+\sqrt{\left(m-4\right)^2}\)
\(=\left|m+1\right|+\left|m-4\right|\)
\(=\left|m+1\right|+\left|4-m\right|>=\left|m+1+4-m\right|=5\)
=>Amin=5
7 tháng 6 2021
\(\Delta=4m^2+69\ge0\Leftrightarrow\begin{matrix}m\ge\dfrac{\sqrt{69}}{2}\\m\le-\dfrac{\sqrt{69}}{2}\end{matrix}\)
viet : \(\left\{{}\begin{matrix}x_1+x_2=7\\x_1x_2=-\left(m^2+5\right)\end{matrix}\right.\)
ta có : \(A=\left(x_1+x_2\right)^2-x_1x_2+2m=49+m^2+5+2m=m^2+2m+54\)
vì \(m\ge\dfrac{\sqrt{69}}{2}\Rightarrow m^2+2m+54\ge\dfrac{69+2\sqrt{69}+216}{4}\) hay \(A\ge\dfrac{69+2\sqrt{69}+216}{4}\)
21 tháng 4 2022
a) Xét pt đã cho có \(a=m^2+m+1\); \(b=-\left(m^2+2m+2\right)\); \(c=-1\)
Nhận thấy rằng \(ac=\left(m^2+m+1\right)\left(-1\right)=-\left(m^2+m+1\right)\)
\(=-\left(m^2+2m.\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\right)=-\left(m+\dfrac{1}{2}\right)^2-\dfrac{3}{4}\)
Vì \(-\left(m+\dfrac{1}{2}\right)^2\le0\) và \(-\dfrac{3}{4}< 0\) nên \(-\left(m+\dfrac{1}{2}\right)^2-\dfrac{3}{4}< 0\) hay \(ac< 0\). Vậy pt đã cho luôn có 2 nghiệm trái dấu.
b) Theo câu a, ta đã chứng minh được pt đã cho luôn có 2 nghiệm trái dấu \(x_1,x_2\).
Áp dụng hệ thức Vi-ét, ta có \(S=x_1+x_2=-\dfrac{b}{a}=-\dfrac{-\left(m^2+2m+2\right)}{m^2+m+1}=\dfrac{m^2+2m+2}{m^2+m+1}\)
Nhận thấy \(m^2+m+1\ne0\) nên ta có:
\(\left(m^2+m+1\right)S=m^2+2m+2\) \(\Leftrightarrow Sm^2+Sm+S-m^2-2m-2=0\)\(\Leftrightarrow\left(S-1\right)m^2+\left(S-2\right)m+\left(S-2\right)=0\)(*)
pt (*) có \(\Delta=\left(S-2\right)^2-4\left(S-1\right)\left(S-2\right)\)\(=S^2-4S+4-4\left(S^2-3S+2\right)\)\(=S^2-4S+4-4S^2+12S-8\)\(=-3S^2+8S-4\)
Để pt (*) có nghiệm thì \(\Delta\ge0\) hay \(-3S^2+8S-4\ge0\)\(\Leftrightarrow-3S^2+6S+2S-4\ge0\)\(\Leftrightarrow-3S\left(S-2\right)+2\left(S-2\right)\ge0\) \(\Leftrightarrow\left(S-2\right)\left(2-3S\right)\ge0\)
Ta xét 2 trường hợp:
TH1: \(\left\{{}\begin{matrix}S-2\ge0\\2-3S\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}S\ge2\\S\le\dfrac{2}{3}\end{matrix}\right.\)
TH2: \(\left\{{}\begin{matrix}S-2\le0\\2-3S\le0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}S\le2\\S\ge\dfrac{2}{3}\end{matrix}\right.\Leftrightarrow\dfrac{2}{3}\le S\le2\) (nhận)
Khi \(S=\dfrac{2}{3}\) thì (*) \(\Leftrightarrow\left(\dfrac{2}{3}-1\right)m^2+\left(\dfrac{2}{3}-2\right)m+\dfrac{2}{3}-2=0\)\(\Leftrightarrow-\dfrac{1}{3}m^2-\dfrac{4}{3}m-\dfrac{4}{3}=0\)\(\Leftrightarrow m^2+4m+4=0\)
\(\Leftrightarrow\left(m+2\right)^2=0\) \(\Leftrightarrow m+2=0\) \(\Leftrightarrow m=-2\)
Khi \(S=2\) thì (*) \(\Leftrightarrow\left(2-1\right)m^2+\left(2-2\right)m+2-2=0\)\(\Leftrightarrow m^2=0\)
\(\Leftrightarrow m=0\)
Vậy GTNN của S là \(\dfrac{2}{3}\) khi \(m=-2\) và GTLN của S là \(2\) khi \(m=0\)
VD
21 tháng 3 2022
1, Ta có: \(\Delta'=\left(-m\right)^2-\left(2m-1\right)=m^2-2m+1=\left(m-1\right)^2\ge0\)
Suy ra pt luôn có 2 nghiệm
2, Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=2m-1\end{matrix}\right.\)
\(A=\left(x_1^2+x_2^2\right)-5x_1x_2\\ =\left(x_1+x_2\right)^2-7x_1x_2\\ =\left(2m\right)^2-7\left(2m-1\right)\\ =4m^2-14m+7\)
Đề sai r bạn
\(b,4m^2-14m+7\\ =4\left(m^2-\dfrac{7}{2}m+\dfrac{7}{4}\right)\\ =4\left(m^2-2.\dfrac{7}{4}m+\dfrac{49}{16}-\dfrac{21}{16}\right)\\ =4\left(m-\dfrac{7}{4}\right)^2-\dfrac{21}{4}\ge-\dfrac{21}{4}\)
Dấu "=" xảy ra \(\Leftrightarrow m=\dfrac{7}{4}\)
Vậy m=`7/4` thì A đạt GTNN
21 tháng 3 2022
1: \(\text{Δ}=\left(-2m\right)^2-4\left(2m-1\right)\)
\(=4m^2-8m+4=\left(2m-2\right)^2>=0\forall m\)
Do đó: Phương trình luôn có hai nghiệm
2: \(A=\left(x_1+x_2\right)^2-7x_1x_2\)
\(=\left(-2m\right)^2-7\left(2m-1\right)\)
\(=4m^2-14m+7\)
15 tháng 5 2023
1: Δ=(2m-2)^2-4(2m-5)
=4m^2-8m+4-8m+20
=4m^2-16m+24
=4m^2-16m+16+8
=(2m-4)^2+8>=8>0 với mọi m
=>PT luôn có 2 nghiệm pb
2: Để pt có hai nghiệm trái dấu thì 2m-5<0
=>m<5/2
3: A=(x1+x2)^2-2x1x2
=(2m-2)^2-2(2m-5)
=4m^2-8m+4-4m+10
=4m^2-12m+14
=4(m^2-3m+7/2)
=4(m^2-2m*3/2+9/4+5/4)
=4(m-3/2)^2+5>=5
Dấu = xảy ra khi m=3/2
2
15 tháng 5 2023
`1)` Ptr có: `\Delta'=[-(m-1)]^2-2m+5`
`=m^2-4m+4+2=(m-2)^2+2 > 0 AA m`
`=>` Ptr có `2` nghiệm phân biệt `AA m`
`2)` Ptr có `2` nghiệm trái dấu `<=>ac < 0`
`<=>2m-5 < 0<=>m < 5/2`
`3) AA m` ptr có `2` nghiệm phân biệt
`=>` Áp dụng Viét có: `{(x_1+x_2=-b/a=2m-2),(x_1.x_2=c/a=2m-5):}`
Ta có: `A=x_1 ^2+x_2 ^2`
`<=>A=(x_1+x_2)^2-2x_1.x_2`
`<=>A=(2m-2)^2-2(2m-5)`
`<=>A=4m^2-8m+4-4m+10`
`<=>A=4m^2-12m+14`
`<=>A=(2m-3)^2+5 >= 5 AA m`
`=>A_[mi n]=5`
Dấu "`=`" xảy ra `<=>2m-3=0<=>m=3/2`
\(A=\left|m+1\right|+\left|m-4\right|=\left|m+1\right|+\left|4-m\right|>=\left|m+1+4-m\right|=5\)
Dấu = xảy ra khi -1<=m<=4