
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

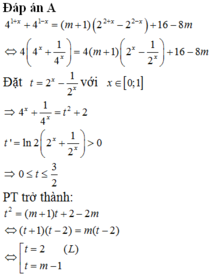
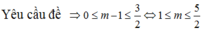

Đáp án D.
Phương trình tương đương với

Đặt 2 x - 1 2 x = t → 4 x + 1 4 x = t 2 + 2 . Xét hàm số t ( x ) = 2 x - 1 2 x trên 0 ; 1 .
Đạo hàm t ' ( x ) = 2 x . ln 2 + ln 2 2 x > 0 , ∀ x ∈ 0 ; 1 ⇒ Hàm số t ( x ) luôn đồng biến trên 0 ; 1 . Suy ra min x ∈ 0 ; 1 t ( x ) = t ( 0 ) = 0 và max x ∈ 0 ; 1 t ( x ) = t ( 1 ) = 3 2 . Như vậy t ∈ 0 ; 3 2 .
Phương trình (1) có dạng:
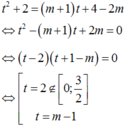
Phương trình (1) có nghiệm t ∈ 0 ; 1 ⇔ phương trình ẩn t có nghiệm t ∈ 0 ; 3 2 ⇔ 0 ≤ m - 1 ≤ 3 2 ⇔ 1 ≤ m ≤ 5 2 . Mà m ∈ ℤ nên m ∈ 1 ; 2 . Tổng tất cả các giá trị nguyên của m bằng 3.

1. Xét x = - 2, thay vào pt ta dc: -1.0 = 4.0 (Hợp lí)
Vậy x = -2 là 1 nghiệm của pt
Xét x \(\ne\)- 2, ta có: x + 1 = 2 - x
<=> 2x = 1 <=> x = 1/2
Vậy S = {1/2; -2}
2. a. \(2\left(m+\frac{3}{5}\right)-\left(m+\frac{13}{5}\right)=5\)
<=> \(2m+\frac{6}{5}-m-\frac{13}{5}=5\)
<=> m = \(\frac{32}{5}\)
b. \(2\left(3m+1\right)+\frac{1}{4}-\frac{2\left(3m-1\right)}{5}+3m+\frac{1}{5}=5\)
<=> \(6m+2+\frac{1}{4}-\frac{6m-2}{5}+3m+\frac{1}{5}=5\)
<=> \(6m-\frac{6m-2}{5}+3m=5-2-\frac{1}{4}-\frac{1}{5}\)
<=> \(9m-\frac{6m-2}{5}=\frac{51}{20}\)
<=> \(\frac{45m-6m+2}{5}=\frac{51}{20}\)
<=> \(20\left(39m+2\right)=51.5\)
<=> 780m + 40 = 255
<=> 780m = 215
<=> m = \(\frac{43}{156}\)

Đáp án là B
Phương trình tương đương với
![]()
![]()
![]()
Xét hàm ![]() Ta có
Ta có ![]() đồng biến
đồng biến
Mà ![]() suy ra
suy ra
![]()
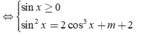
![]()
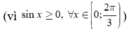
![]()
![]()
Đặt u = cosx, 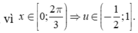
Khi đó phương trình trở thành ![]()
Xét ![]()
![]()
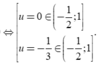
Bảng biến thiên
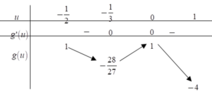
Dựa vào bảng biến thiên suy ra phương trình có nghiệm khi
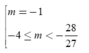
![]()