DQ
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LD
2
2 tháng 11 2019
a)
vì\(74^{30}=\left(....4^2\right)^{15}=....6^{15}=....6\)
2 tháng 11 2019
\(49^{31}=\left(...9\right)\)
\(37^{32}=\left(...1\right)\)
\(58^{33}=\left(...8\right)\)
\(232^{35}=\left(....7\right)\)
22 tháng 11 2016
1)Vì n>1\(\Rightarrow\)n có dạng 2k,2k+1(k\(\in\)N*)
Xét n có dạng 2k\(\Rightarrow5^{2k}\)=\(25^k\) có 2 chữ số tận cùng là 25
Xét n có dạng 2k+1
\(\Rightarrow5^{2k+1}\)=\(5^{2k}\cdot5=25^k\cdot5\)
Vì \(25^k\) có 2 chữ số tận cùng là 25
\(\Rightarrow\)\(25^k\cdot5\) có 3 chữ số tận cùng là 125
\(\Rightarrow\)\(25^k\cdot5\) có 2 chữ số tận cùng là 25
Vậy trong trường hợp nào thì \(5^n\) luôn có 2 chữ số tận cùng là 25(n>1)
CL
4
10 tháng 4 2016
chữ số tận cùng của 234^5^6^7 là 6
chữ số tận cùng của579^6^7^5 là 1.
tích nha bn.
10 tháng 4 2016
234^5^6^7 có chữ số tận cùng là 6
579^6^7^5 có chữ số tận cùng là 1
TD
0
5 tháng 6 2017
Ta thấy:Các số có tận cùng là 0;1;5;6 khi nâng lên bất kì lũy thừa bậc nào đều có tận cùng là chính nó.
=>a)=...5
b)=...0.
c=...6
d=...1.
e)9^18=(9^2)^9=81^9=...1
13 tháng 1 2020
72019\=72016 +3 =72.2 504.73=...11009 . 73=...1.7.7.7=...9.7=...3
vậy chữ số tận cùng là 3
#Học-tốt
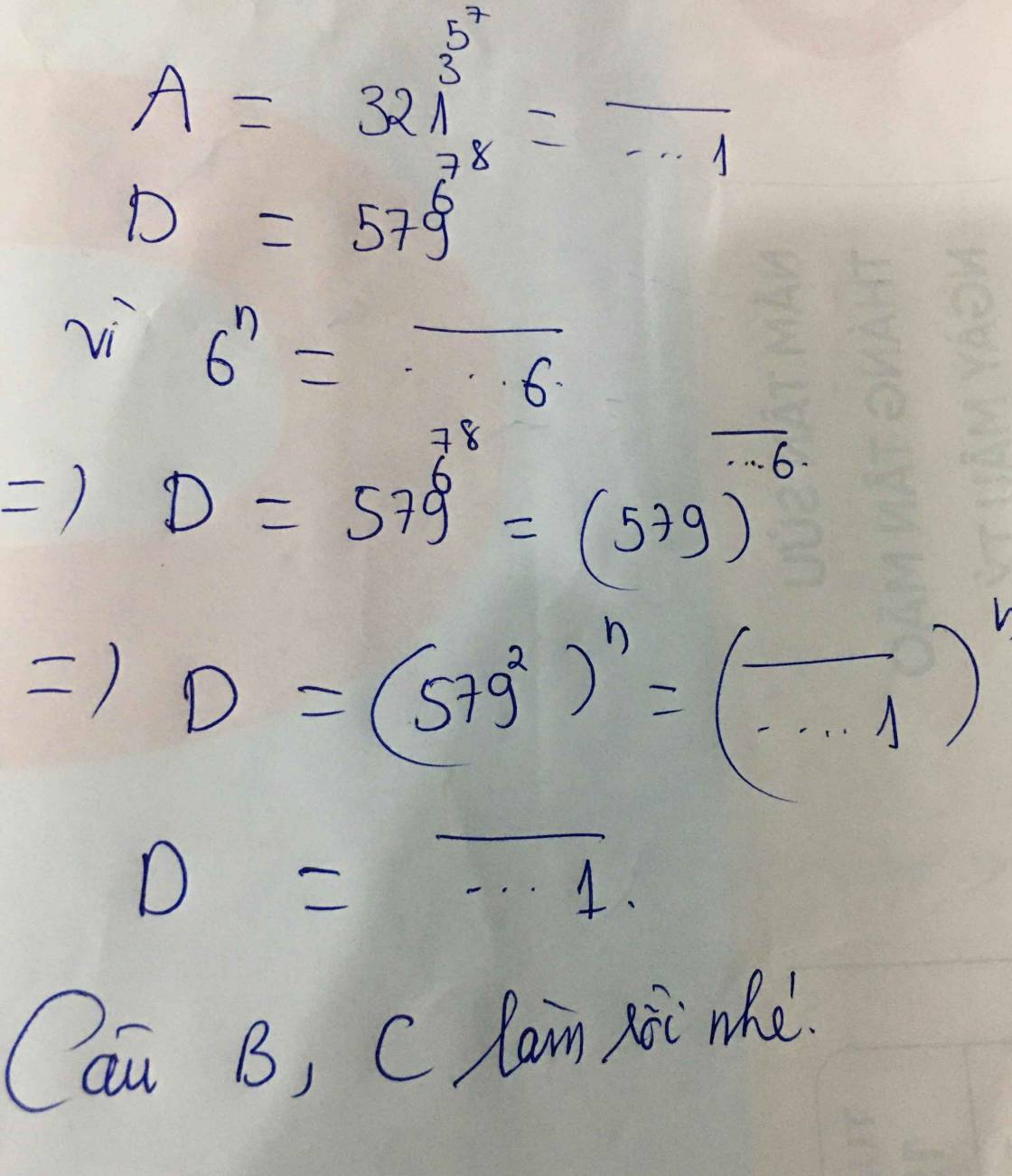
Ta có:
...92n = ...1
...92n+1 = ...9
Mà 31 là số lẻ
=> 4931 = ...9
Ta có:
...34n+1 = ...3
=> ...34n+3 = ...7
Mà 35 chia 4 dư 3
=> 2335 = ... 7
Ta có:
\(234^{5^{6^7}}\)có số mũ 5 nên khi lũy thừa số mũ đó lên sẽ là số lẻ
=> \(5^{6^7}=2m+1\)
Mà
...42n = ...6
...42n+1 = ...4
=> \(234^{5^{6^7}}=...4\)