
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Các tam giác cân trên hình 112:
-ΔADE cân tại A: có các cạnh bên là AD và AE; cạnh đáy: DE; góc D và góc E là hai góc ở đáy; góc A là góc ở đỉnh
-ΔABC cân tại A: có các cạnh bên là AB và AC; cạnh đáy: BC; góc B và góc C là hai góc ở đáy; góc A là góc ở đỉnh
-ΔAHC cân tại A: có các cạnh bên là AH và AC; cạnh đáy: HC; góc H và góc C là hai góc ở đáy; góc A là góc ở đỉnh

+) Xét tam giác ABC có AB = AC nên tam giác ABC cân tại A.
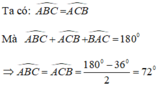
+) Xét tam giác ABD có góc ABC là góc ngoài tam giác tại đỉnh B nên:
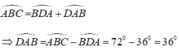
Do tam giác ABD có: 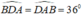 nên tam giác ABD cân tại B.
nên tam giác ABD cân tại B.
+) Ta có:
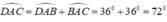
Tam giác ADC có: 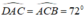 nên tam giác ADC cân tại D.
nên tam giác ADC cân tại D.
+) Xét tam giác ACE có góc ACB là góc ngoài tam giác tại đỉnh C nên:
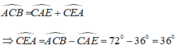
Do tam giác ACE có: 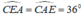 nên tam giác ACE cân tại C.
nên tam giác ACE cân tại C.
+) Ta có:
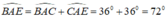
Tam giác ABE có: 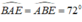 nên tam giác ABE cân tại E.
nên tam giác ABE cân tại E.
+) Tam giác ADE có: 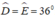 nên tam giác này cân tại A.
nên tam giác này cân tại A.
Vậy có tất cả 6 tam giác đều là: ABD, ABC, ACE, AEB; ADC và ADE.

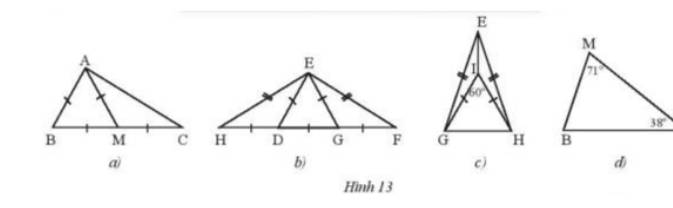
a) Tam giác ABM là tam giác đều do có 3 cạnh bằng nhau
Tam giác AMC cân tại M do AM = MC
b) Tam giác EDG là tam giác đều do có 3 cạnh bằng nhau
Tam giác EHF cân tại E do EH = EF
Tam giác EDH cân tại D do DH = DE
c) Tam giác EGF cân tại G do GE = GF
Tam giác IHG đều do là tam giác cân có 1 góc = 60°
Tam giác EHG cân tại E do EG = EH
d) Tam giác MBC không cân và không đều vì 3 góc có số đo khác nhau.

Do MA và MC không đổi =>Để AM^2+BM^2+CM^2 nhỏ nhất =>AM là đường cao của tam giác ABC (1)
Mà ABC vuông cân =>M là trung điểm của BC
Kẻ MI vuông góc với AB,MK vuông góc với AC
suy ra MI // Ak,AI // MK suy ra AIMK là hình chữ nhật
Ta có :AM^2+BM^2+CM^
=AI^2+IM^2+IM^2+IB^2+CK^2+MK^2
=2AI^2+2IM^2+AM^2
=2*(AI^2+IM^2)+AM^2
=3AM^2
Từ (1) => AM^2+BM^2+c

ΔDMC cân tại M
ΔDMB cân tại M
ΔEMB cân tại M
ΔEMC cân tại M
ΔEMD cân tại M
 Tìm các tam giác cân trên hình vẽ sau
Tìm các tam giác cân trên hình vẽ sau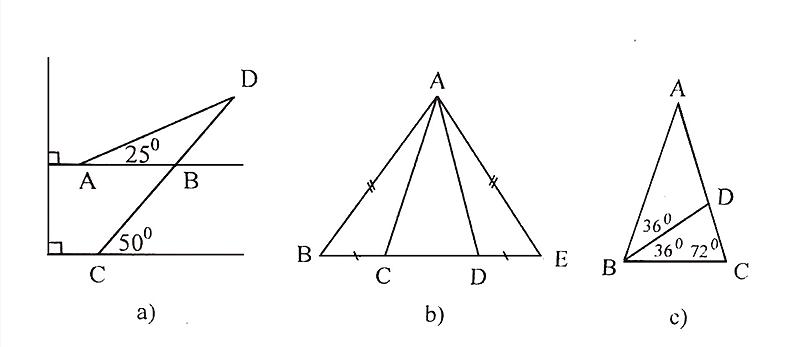 Giúp mình hình b với
Giúp mình hình b với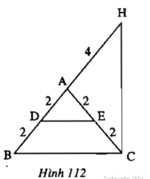
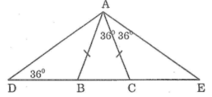
Xét ΔBDC có:
\(\widehat{BDC}+\widehat{BCD}+\widehat{DBC}=180^o\\ \Rightarrow36^o+72^o+\widehat{BDC}=180^o\\ \Rightarrow\widehat{BDC}=72^o\)
Vì \(\widehat{BDC}=\widehat{BCD}\) nên ΔBDC cân tại B
Xét ΔABC có:
\(\widehat{ACB}+\widehat{ABC}+\widehat{BAC}=180^o\\ \Rightarrow36^o+72^o+\widehat{ABC}=180^o\\ \Rightarrow\widehat{ABC}=72^o\)
Vì \(\widehat{ABC}=\widehat{ACB}\) nên ΔABC cân tại A
36