
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tính cạnh đáy BC của tam giác cân ABC trên các hình dưới đây. Trên hình bên trái: AH = 7cm; HC = 2cm
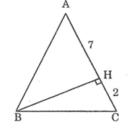
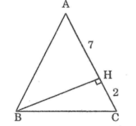

Tam giác ABC cân tại A ta có: AB = AC = CH + HA = 2 + 7 =9
Trong tam giác vuông BHA, ta có ∠(BHA) =90°
Áp dụng định lí pitago, ta có: AB2=BH2+HA2
Suy ra: BH2=AB2-AH2=92-72=81-49=32
Trong tam giác vuông BHC, ta có ∠(BHC) =90°
Áp dụng định lí pitago ta có: BC2=BH2+HC2 mà BH2 = 32, HC2 = 22 = 4
BC2 =32 + 4 =36 ⇒ BC = √36 = 6 cm
Tính cạnh đáy BC của tam giác cân ABC trên các hình dưới đây. Trên hình bên phải: AH = 4cm; HC = 1cm
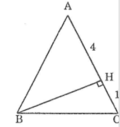

Tam giác ABC cân tại A nên ta có: AB=AC= AH + HC =4+1=5
Trong tam giác vuông BHA ta có ∠(BHA) =90°
Áp dụng định lí pitago, ta có: AB2=BH2+HA2
Suy ra: BH2=AB2-AH2=52-42=25-16=9
Trong tam giác vuông BHC, ta có ∠(BHC) =90°
Áp dụng định lí pitago ta có: BC2=BH2+HC2
BC2=9+1=10 =>BC=√10

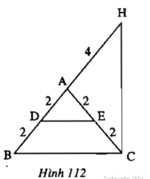
Các tam giác cân trên hình 112:
-ΔADE cân tại A: có các cạnh bên là AD và AE; cạnh đáy: DE; góc D và góc E là hai góc ở đáy; góc A là góc ở đỉnh
-ΔABC cân tại A: có các cạnh bên là AB và AC; cạnh đáy: BC; góc B và góc C là hai góc ở đáy; góc A là góc ở đỉnh
-ΔAHC cân tại A: có các cạnh bên là AH và AC; cạnh đáy: HC; góc H và góc C là hai góc ở đáy; góc A là góc ở đỉnh

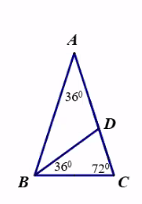
Xét ΔBDC có:
\(\widehat{BDC}+\widehat{BCD}+\widehat{DBC}=180^o\\ \Rightarrow36^o+72^o+\widehat{BDC}=180^o\\ \Rightarrow\widehat{BDC}=72^o\)
Vì \(\widehat{BDC}=\widehat{BCD}\) nên ΔBDC cân tại B
Xét ΔABC có:
\(\widehat{ACB}+\widehat{ABC}+\widehat{BAC}=180^o\\ \Rightarrow36^o+72^o+\widehat{ABC}=180^o\\ \Rightarrow\widehat{ABC}=72^o\)
Vì \(\widehat{ABC}=\widehat{ACB}\) nên ΔABC cân tại A

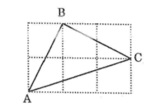
Đặt độ dài cạnh ô vuông là 1 (đơn vị chiều dài)
Áp dụng định lí pitago ta có:
AB2=12+22=1+4=5
BC2=12+22=1+4=5
AC2=32+12=9+1=10
Suy ra: AC2=AB2+BC2
Áp dụng định lí pitago đảo ta có tam giác ABC vuông tại B
Lại có: AB2=BC2=5 suy ra: AB = BC. Do đó, tam giác ABC là tam giác cân tại B.
Vậy tam giác ABC vuông cân tại B


a) Ta có: EF//BC(gt) =>\(\left\{{}\begin{matrix}\text{^EOB = ^OBC (SLT)}\\\text{ ^FOC = ^OCB (SLT)}\\\text{^AEF = ^B (Đồng vị)}\\\text{^AFE = ^C (Đồng vị)}\end{matrix}\right.\)
Có: ^OBC = ^OBA ( BF là phân giác ^B)
mà: ^EOB = ^OBC (cmt)
=> ^EOB = ^OBA => tam giác EBO cân tại E
Có: ^OCA = ^OCB ( BF là phân giác ^B)
mà: ^FOC = ^OCB (cmt)
=> ^FOC = ^OCA => tam giác FCO cân tại E
Ta có: ^AEF = ^B (cmt)
^AFE = ^C (cmt)
Mà ^B = ^C (tam giác ABC cân tại A)
=> ^AEF = ^AFE => tam giác AEF cân tại A
Có : ^ABF = ^CBF = \(\dfrac{1}{2}\) ^B ( BF là phân giác ^B)
^ACE = ^BCE = \(\dfrac{1}{2}\) ^B ( CF là phân giác ^C)
mà : ^B = ^C (tam giác ABC cân tại A)
=> ^ACE = ^ABF = ^CBF = ^BCE
Xét tg OBC có: ^OBC = ^OCB (^CBF = ^BCE) => tg OBC cân tại O
Xét tam giác FCO và tam giác EBO có:
^FOC = ^FOB ( đối đỉnh)
^FCO = ^EBO (^ABF = ^ACE)
OB = OC ( tg OBC cân tại O )
=> tam giác FCO = tam giác EBO(g-c-g)
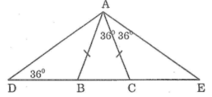
 Tìm các tam giác cân trên hình vẽ sau
Tìm các tam giác cân trên hình vẽ sau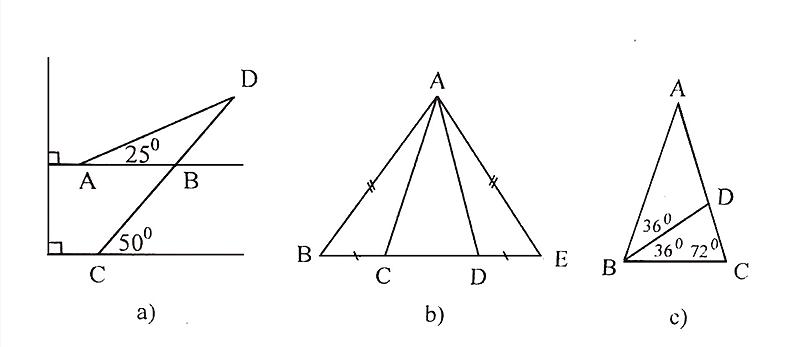 Giúp mình hình b với
Giúp mình hình b với
+) Xét tam giác ABC có AB = AC nên tam giác ABC cân tại A.
+) Xét tam giác ABD có góc ABC là góc ngoài tam giác tại đỉnh B nên:
Do tam giác ABD có: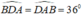 nên tam giác ABD cân tại B.
nên tam giác ABD cân tại B.
+) Ta có:
Tam giác ADC có: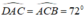 nên tam giác ADC cân tại D.
nên tam giác ADC cân tại D.
+) Xét tam giác ACE có góc ACB là góc ngoài tam giác tại đỉnh C nên:
Do tam giác ACE có: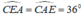 nên tam giác ACE cân tại C.
nên tam giác ACE cân tại C.
+) Ta có:
Tam giác ABE có: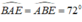 nên tam giác ABE cân tại E.
nên tam giác ABE cân tại E.
+) Tam giác ADE có: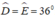 nên tam giác này cân tại A.
nên tam giác này cân tại A.
Vậy có tất cả 6 tam giác đều là: ABD, ABC, ACE, AEB; ADC và ADE.