Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Nếu m = 0 thì bất phương trình nghiệm đúng với mọi x;
+ Nếu m = -2 thì bất phương tình trở thành – 4x + 2 > 0, không nghiệm đúng với mọi x.
+ Nếu m ≠ 0 và m ≠ -2 thì bất phương trình nghiệm đúng với mọi x khi và chỉ khi
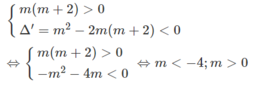
Đáp số: m < -4; m ≥ 0

Để pt có 2 nghiệm phân biệt thì \(\Delta'=m^2-\left(m+2\right)>0\Leftrightarrow\left(m+1\right)\left(m-2\right)>0\Leftrightarrow\left[{}\begin{matrix}m>2\\m< -1\end{matrix}\right.\). (1)
Khi đó theo hệ thức Viète ta có \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=m+2\end{matrix}\right.\).
Ta có \(x_1^3+x_2^3=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=\left(2m\right)^3-3.2m.\left(m+2\right)=8m^3-6m^2-12m\).
Do đó \(8m^3-6m^2-12m\le16\Leftrightarrow\left(m-2\right)\left(8m^2+10m+8\right)\le0\Leftrightarrow m\le2\)
(do \(8m^2+10m+8=2\left(2m+\dfrac{5}{4}\right)^2+\dfrac{39}{8}>0\forall m\)).
Kết hợp vs (1) ta có m < -1.

Ta có: x 2 + 1 x 2 − 2 m x + 1 x + 1 = 0
x + 1 x 2 − 2 m x + 1 x − 1 = 0 ( 1 )
Đặt x + 1 x = t , t ≥ 2 ta được t 2 − 2 m t − 1 = 0 ( 2 )
Phương trình (2) luôn có hai nghiệm t 1 < 0 < t 2 d o a , c = - 1 < 0 a ⇒ phương trình (1) có nghiệm khi và chỉ khi phương trình (2) có ít nhất một nghiệm t sao cho t ≥ 2 , hay ít nhất một trong hai số 2; −2 phải nằm giữa hai nghiệm t 1 , t 2 hay f ( 2 ) ≤ 0 f ( − 2 ) ≤ 0 ⇔ 3 − 4 m ≤ 0 3 + 4 m ≤ 0 ⇔ m ≥ 3 4 m ≤ − 3 4

Đáp án cần chọn là: B

\(\Delta'=m^2-\left(m+2\right)\ge0\Leftrightarrow\left[{}\begin{matrix}m\ge2\\m\le-1\end{matrix}\right.\) (1)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=m+2\end{matrix}\right.\)
\(x_1^3+x_2^3\le16\Leftrightarrow\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)\le16\)
\(\Leftrightarrow8m^3-6m\left(m+2\right)-16\le0\)
\(\Leftrightarrow4m^3-3m^2-6m-8\le0\)
\(\Leftrightarrow\left(m-2\right)\left(4m^2+5m+4\right)\le0\)
\(\Leftrightarrow\left(m-2\right)\left[\left(2m+\dfrac{5}{4}\right)^2+\dfrac{39}{16}\right]\le0\)
\(\Leftrightarrow m\le2\) (2)
Kết hợp (1); (2) \(\Rightarrow\left[{}\begin{matrix}m=2\\m\le-1\end{matrix}\right.\)

Để phương trình x 2 - 2 m x + m + 2 = 0 có hai nghiệm dương phân biệt
⇔ Δ ' > 0 S > 0 P > 0 ⇔ − m 2 − 1. m + 2 > 0 2 m > 0 m + 2 > 0 ⇔ m 2 − m − 2 > 0 m > 0 m > − 2 ⇔ m < − 1 , m > 2 m > 0 m > − 2
Vậy: m > 2
Đáp án cần chọn là: A

Lời giải:
PT có 2 nghiệm pb khi:
$\Delta'=m^2+m(2m+1)>0\Leftrightarrow m(3m+1)>0\Leftrightarrow m>0$ hoặc $m< \frac{-1}{3}(*)$
Theo định lý Viet: \(\left\{\begin{matrix} x_1+x_2=2\\ x_1x_2=\frac{-(2m+1)}{m}\end{matrix}\right.\) . Khi đó:
$x_1^2+2x_1x_2^2+3x_2^2=4x_1+5x_2-1$
$\Leftrightarrow (x_1+x_2)^2+2x_2^2=4(x_1+x_2)+x_2-1$
$\Leftrightarrow 4+2x_2^2=7+x_2$
$\Leftrightarrow 2x_2^2-x_2-3=0$
$\Leftrightarrow x_2=\frac{3}{2}$ hoặc $x_2=-1$
$x_2=\frac{3}{2}$ thì $x_1=\frac{1}{2}$
$\frac{-(2m+1)}{m}=x_1x_2=\frac{3}{4}\Leftrightarrow m=\frac{-4}{11}$
$x_2=-1$ thì $x_1=3$
$\frac{-(2m+1)}{m}=x_1x_2=-3\Leftrightarrow m=1$
(hai giá trị trên đều thỏa mãn)
Ohh em làm cách khác vẫn ra thế này! Thầy nhiệt tình thật !
Ptr có: `\Delta'=m^2-(7m^2-6m)=m^2-7m^2+6m=-6m^2+6m`
`a)` Ptr vô nghiệm `<=>\Delta' < 0`
`<=>-6m^2+6m < 0`
`<=>m in (-oo;0)uu(1;+oo)`
`b)` Ptr có nghiệm `<=>\Delta' >= 0`
`<=>-6m^2+6m >= 0`
`<=>m in [0;1]`
weo