Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Tiếp tuyến của \(\left(C_m\right)\) tại điểm có hoành độ x = 1 có phương trình :
\(y=\left(m-2\right)\left(x-1\right)+3m-2=\left(m-2\right)x+3m\)
Yêu cầu của bài toán khi và chỉ khi \(\begin{cases}m-2=3\\2m\ne10\end{cases}\) vô nghiệm
Vậy không tồn tại m thỏa mãn yêu cầu bài toán
b. Ta có \(y'=3\left(x^2-\frac{4}{3}x+\frac{4}{9}\right)+m-\frac{7}{3}=3\left(x-\frac{2}{3}\right)^2+m-\frac{7}{3}\)
Suy ra \(y'\ge m-\frac{7}{3}\)
Tiếp tuyến tại điểm có hoành độ \(x=\frac{2}{3}\) có hệ số góc nhỏ nhất và hệ số góc có giá trị \(k=m-\frac{7}{3}\)
Yêu cầu bài toán \(\Leftrightarrow k.2=-1\Leftrightarrow\left(m-\frac{7}{3}\right).2=-1\Leftrightarrow m=\frac{11}{6}\)

+Ta có đạo hàm y’ = 3x2- 6mx+ 3( m+ 1) .
Do K thuộc ( C) và có hoành độ bằng -1, suy ra K( -1; -6m-3)
Khi đó tiếp tuyến tại K có phương trình
∆: y= ( 9m+ 6) x+ 3m+ 3
Đường thẳng ∆ song song với đường thẳng d
⇒ 3 x + y = 0 ⇔ y = - 3 x ⇔ 9 m + 6 = - 3 3 m + 3 ≠ 0 ⇔ m = - 1 m ≠ - 1
Vậy không tồn tại m thỏa mãn đầu bài.
Chọn D.

Ta có \(M\left(-1;-2\right)\)
Phương trình của (C) tại M là \(\Delta:y=y'\left(-1\right)\left(x+1\right)-2\)
hay \(\Delta:y=9x+7\)
\(\Delta\) // d \(\Leftrightarrow\begin{cases}m^2+5=9\\3m+1\ne7\end{cases}\) \(\Leftrightarrow\begin{cases}m=\pm2\\m\ne2\end{cases}\) \(\Leftrightarrow m=-2\)

Đáp án D
Cách giải:
Xét phương trình hoành độ giao điểm của (C) và đường thẳng y = 2x + m:
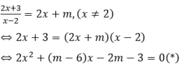
Dễ dàng kiểm tra được x = 2 không phải nghiệm của phương trình (*) với mọi m
Để phương trình (*) có 2 nghiệm phân biệt x1, x2 thì Δ > 0 ⇔ (m - 6)2 + 8(2m + 3) > 0 ⇔ m2 + 4m + 60 > 0, luôn đúng
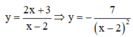
Tiếp tuyến của (C) tại hai điểm giao song song với nhau
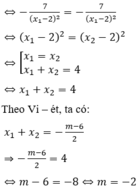
Vậy, có 1 giá trị thực của tham số m thỏa mãn yêu cầu đề bài.
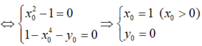

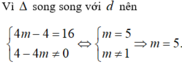

y’ = x² – 4x + 3 = 0 ⇔ x =1, x = 3 y” = 2x – 4, y”(1) = -2, y”(3) = 2 Suy ra hàm số đạt cực tiểu tại x = 3. Phương trình tiếp tuyến tại điểm cực tiểu có hệ số góc là y'(3) = 0. Do đó, tiếp tuyến song song với trục hoành. Chọn B
y’= x2 – 4x + 3 = 0 ⇔ x = 1, x = 3
y’’ = 2x -4, y’’(1) = -2, y’’(3) = 2
Suy ra hàm số đạt cực tiểu tại x = 3.
Phương trình tiếp tuyến tại điểm cực tiểu có hệ số góc y’(3) = 0. Do đó tiếp tuyến song song với trục hoành.
Chọn đáp án 2