Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo
a)
-7x2(3x - 4y)
= -7x2.3x + 7x2ư.4y
= -21x2 + 28x2y
b)
(x - 3)(5x - 4)
= x.5x - x.4 - 3.5x + 3.4
= 5x2 - 4x - 15x + 12
= 5x2 - 19x + 12
c)
(2x - 1)2 = 4x2 - 4x + 1
d)
(x + 3)(x - 3) = x2 - 32 = x2 - 9

a: \(=15x^5y^3-6x^4y^2-6x^3y^3\)
c: \(=2x^4-2x^2-3x^3+3x+x^2-1\)
\(=2x^4-3x^3-x^2+3x-1\)

Bài 1:
\(a,=6x^2+6x\\ b,=15x^3-10x^2+5x\\ c,=6x^3+12x^2\\ d,=15x^4+20x^3-5x^2\\ e,=2x^2+3x-2x-3=2x^2+x-3\\ f,=3x^2-5x+6x-10=3x^2+x-10\)
Bài 2:
\(a,\Leftrightarrow3x^2+3x-3x^2=6\\ \Leftrightarrow3x=6\Leftrightarrow x=2\\ b,\Leftrightarrow6x^2+3x-6x^2+9x-2x-3=10\\ \Leftrightarrow10x=13\Leftrightarrow x=\dfrac{13}{10}\)

Bài 3:
\(\Leftrightarrow x^3+64-x^3+25x=264\)
hay x=8
\(1,C=6x^2+23x-55-6x^2-23x-21=-76\\ 2,=\left(2x^4-x^2+2x^3-x-6x^2+6-3\right):\left(2x^2-1\right)\\ =\left[\left(2x^2-1\right)\left(x^2+x-6\right)-3\right]:\left(2x^2-1\right)\\ =x^2+x-6\left(dư.-3\right)\\ 3,\Leftrightarrow x^3+64-x^3+25x=264\\ \Leftrightarrow25x=200\Leftrightarrow x=8\)

f: \(=\dfrac{2x^3-10x^2-11x^2+55x+12x-60}{x-5}=2x^2-11x+12\)

a) \(\left(5x^2-2x+1\right)\left(2x^2-3x\right)\)
\(=10x^4-15x^3-4x^3+6x^2+2x^2-3x\)
\(=10x^4-19x^3+8x^2-3x\)

a)(5x2-2x+1).(2x2-3x)
=10x4-4x3+2x2-15x3+6x2-3x
=10x4-19x3+8x2-3x
b)(18x4y3-6x2y3+12x3y4z):6x2y3
=(18x4y3:6x2y3)-(6x2y3:6x2y3)+(12x3y4z:6x2y3)
=3x2y-xy+2xyz

a) \(\left(5x-4y^3\right)\left(2x^2-1+y\right)=10x^3-5x+5xy-8x^2y^3+4y^3-4y^4=-4y^4+10x^3+4y^3-8x^2y^3+5xy-5x\)
b) \(\left(x-3\right)\left(2x-1\right)-\left(2x-7\right)x=2x^2-7x+3-2x^2+7x=3\)

a: \(=\dfrac{2\left(x+2\right)\left(x-1\right)}{x+2}=2x-2\)
b: \(=\dfrac{2x^3+x^2-6x^2-3x+2x+1}{2x+1}=x^2-3x+1\)
c: \(=\dfrac{x^3+2x^2-2x^2-4x+2x+4}{x+2}=x^2-2x+2\)
d: \(=\dfrac{x^2\left(x-3\right)}{x-3}=x^2\)

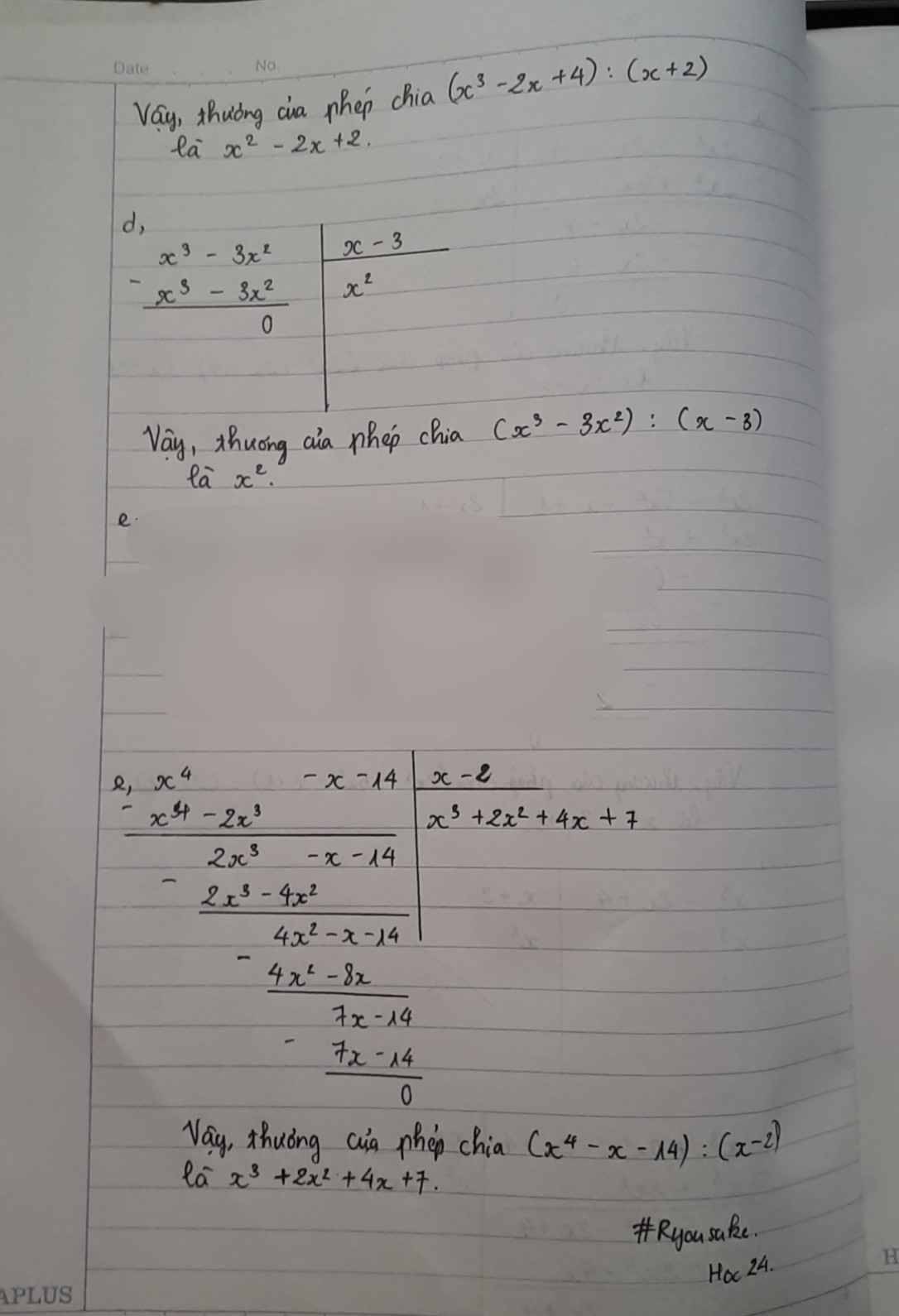

\(a,=-21x^3+28x^2y\\ b,=5x^2-4x-15x+12=5x^2-19x+12\\ c,=4x^2-4x+1\\ d,=49-x^2\)