Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

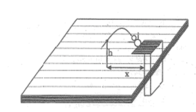
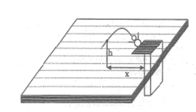
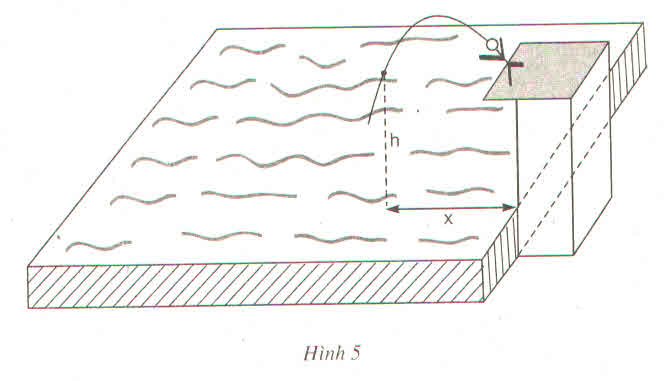
Khi vận động viên chạm mặt nước nghĩa là h = 0m
Ta có: 0 = - x - 1 2 + 4 ⇔ x 2 -2x -3 =0
∆ ' = b ' 2 – ac = - 1 2 -1.(-3) =1 +3 = 4 > 0
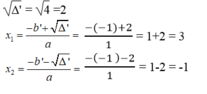
Vì khoảng cách không thể mang giá trị âm nên x=3m

Khi vận động viên ở độ cao 3m nghĩa là h =3m
Ta có: 3 = - x - 1 2 + 4 ⇔ x - 1 2 – 1=0 ⇔ x 2 – 2x = 0
⇔ x(x – 2) = 0 ⇔ x=0 hoặc x – 2 =0 ⇔ x = 0 hoặc x = 2
Vậy x = 0m hoặc x = 2m

a) \(3=-\left(x-1\right)^2+4\Leftrightarrow x^2-2x=0\)
Suy ra \(x_1=0;x_2=2\)
b) Khi vận động viên chạm mặt nước thì \(h=0\).
Do đó \(-\left(x-1\right)^2+4=0\) hay \(x^2-2x-3=0\)
Suy ra \(x_1=-1;x_2=3\)
Vì khoảng cách không âm nên \(x_2=3\left(m\right)\)

Gọi k/c từ mặt hồ tới đáy hồ là x (dm)
Ta có :
chiều dài của hoa sen là x+2 (dm)
áp dụng định lí pytago ta có
x^2+8^2=(x+2)^2
x^2+64=x^2+4x+4
60=4x
x=15
Vậy độ sâu của hồ là 15 dm
Gọi OA là độ dài cây sen
OB là độ sâu của hố
Do gió thổi bông sen chạm mặt nước cách thân cây ở vị trí cũ là 8 dm nên ta có
\(OC=OA=OB+2\)
Và BC = 8 dm
Xét tam giác OBC vuông tại A
Ta có \(OC^2=BC^2+OB^2\)( Định lý pytago )
\(\left(OB+2\right)^2=8^2+OB^2\)
\( \left(OB+2\right)\left(OB+2\right)=64+OB^2\)
\(OB^2 +2OB+2OB+4=64+OB^2\)
\(4OB=60\)
\(\Rightarrow OB=60\div4=15dm\)
VÂY ĐỘ DÀI CỦA HỒ NƠI CÓ BÔNG SEN LÀ 15 DM

a, Sau 2 giây vật cách mặt đất \(200-5\cdot2^2=180\left(m\right)\)
b, Thay \(s=200\Leftrightarrow t=\sqrt{\dfrac{200}{5}}=2\sqrt{10}\approx6\left(giây\right)\)
Vậy sau khoảng 6 giây thì vật chạm đất

Là \(\tan35^0\cdot5,5+\dfrac{5,5}{\cos35^0}\approx10,57\left(m\right)=1057\left(cm\right)\left(C\right)\)