Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
`100 dm = 10 m`.
Thể tích là: `1/3 xx 30 xx 10 = 100 m^3 => A`.
Diện tích toàn phần: `42 xx 3 + 30 = 152 cm^2.`
`=> D`.
1, Chọn đáp án C.
Ta có: V= \(\dfrac{1}{3}\)S.h
\(\Rightarrow\) 126 = \(\dfrac{1}{3}\)S.6
\(\Rightarrow\) S = 126 : 2 = 63\(\left(cm^3\right)\)
2, Chọn đáp án D
ĐKXĐ: x≠1 ; x≠3
Khi đó : \(\dfrac{x-5}{x-1}+\dfrac{2}{x-3}=1\)
\(\Leftrightarrow\dfrac{\left(x-5\right)\left(x-3\right)}{\left(x-1\right)\left(x-3\right)}+\dfrac{2\left(x-1\right)}{\left(x-1\right)\left(x-3\right)}=\dfrac{\left(x-1\right)\left(x-3\right)}{\left(x-1\right)\left(x-3\right)}\)
\(\Rightarrow\) (x−5) (x−3) + 2 (x−1) = (x−1) (x−3)
\(\Leftrightarrow\) \(x^2-8x+15+2x-2=x^2-4x+3\)
\(\Leftrightarrow\) −8x + 2x + 4x = 3 − 15 + 2
\(\Leftrightarrow\) −2x = −10
\(\Leftrightarrow\) x = 5 ( thỏa mãn ĐKXĐ )
Vậy S = \(\left\{5\right\}\)
Ta có:
\(V=\dfrac{1}{3}.S.h\Rightarrow S=\dfrac{V.3}{h}\)
\(\Rightarrow S=\dfrac{126.3}{6}=63cm^2\)
Vậy chọn phương án (C)63cm2
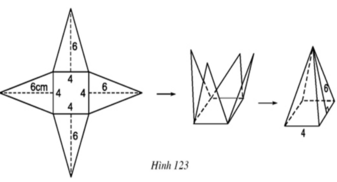
a) Số các mặt bằng nhau trong một hình chóp tứ giác đều là 4
b) Diện tích mỗi mặt tam giác là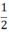 
. 4.6 = 12 cm2.
c) Diện tích đáy của hình chóp đều là 4.4 = 16 cm2.
d) Tổng diện tích tất cả các mặt bên của hình chóp đều là 12.4 = 48 cm2.
a) Số các mặt bằng nhau trong một hình chóp tứ giác đều là 4
b) Diện tích mỗi mặt tam giác là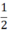 
. 4.6 = 12 cm2.
c) Diện tích đáy của hình chóp đều là 4.4 = 16 cm2.
d) Tổng diện tích tất cả các mặt bên của hình chóp đều là 12.4 = 48 cm2.
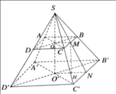
a: S.ABC là hình chóp đều
=>SA=SB=SC và AB=AC=BC
ΔSAB cân tại S có SM là trung tuyến
nên SM vuông góc AB
=>ΔSMA vuông tại M
\(MA=\sqrt{SA^2-SM^2}=2\left(cm\right)\)
=>BA=2*2=4cm=BC=AC
b: \(S_{Xq}=\dfrac{1}{2}\left(4+4+4\right)\cdot5=6\cdot5=30\left(cm^2\right)\)
c: \(S_{tp}=30+4^2\cdot\dfrac{\sqrt{3}}{4}=30+4\sqrt{3}\left(cm^2\right)\)
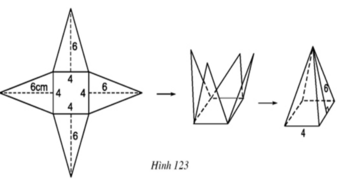
Ta có: V = 1/3 .S.h mà V = 126 ( c m 3 ) ,h = 6cm nên :
126 = 1/3 .S.6 ⇒ S = 126 :2 = 63 ( c m 2 )
Vậy chọn đáp án C