Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

GIAP+NGO+AP+O=2015 Ta có: G.1000 +I.100+AP+N.100+G.10+O+AP+O=2015 G.1010+100x(X+N)+2.AB+2.O=2015 Ta thấy; G.1010+100.(I+N)+2.AP+2.O luôn cho kết quả là 1 số chẵn,mà 2015 là 1 số lẻ nên không có đẳng thức GIAP+NGO+AP+O=2015

- Vì A≠G mà chữ số hàng chục của tổng là 0 nên phép cộng có nhớ 1 sang hàng trăm nên ở hàng trăm: H + N + 1 (nhớ) = 10; nhớ 1 sang hàng nghìn. Do đó H + N = 10 - 1 = 9.
- Phép cộng ở hàng nghìn: N + 1 (nhớ) = 2 nên N = 2 - 1 = 1.
Thay N = 1 ta có: H + 1 = 9 nên H = 9 - 1 = 8
- Phép cộng ở hàng đơn vị: Có 2 trường hợp xảy ra:
* Trường hợp 1: Phép cộng ở hàng đơn vị không nhớ sang hàng chục.
Khi đó: M + O = 0 và A + G = 10.
Ta có bảng: (Lưu ý 4 chữ M, O, A, G phải khác nhau và khác 1; 8)
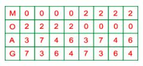
* Trường hợp 2: Phép cộng ở hàng đơn vị có nhớ 1 sang hàng chục.
Khi đó: M + O = 12 và A + G = 9. Ta có bảng:
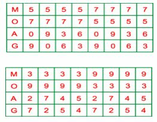
Vậy bài toán có 24 đáp số như trên.

=>100a +10b + c - (100c + 10b + a) = 600 + 10b +3 (điều kiện a,c khác 0) =>100a + 10b + c - 100c - 10b -a =603 + 10b => 99a - 99c = 603 + 10b =>99(a-c) -10b = 603 Những số chia hết cho 99 là :99;198;...;594;693;... => 99(a-c)=693 => a-c = 7 => a-c=9-2;8-1 => 10b = 90 => b=9

Vì N xuất hiện ở những hàng cao nhất và nhiều lần nhất nên N phải bằng 9 để kết quả lớn nhất. Tiếp đó C xuất hiện ở hàng cao nhất còn lại giống M và T nhưng C còn ở hai hàng khác nữa nên C bằng 8. Nếu M là 7 thì T là 6 và ngược lại, kết quả của phép toán không thay đổi. Với lập luận như trên thì H bằng 5, U bằng 4 và G là 3. Từ đó A bằng 2, Y bằng 1 và O là 0.
Vậy ta có 2 đáp số :
8548 + 6493 + 7521 + 80 + 9529 + 9321 - 20 - 11 = 41461
và 8548 + 7493 + 6521 + 80 + 9529 + 9321 - 20 - 11 = 41461
Giaps =1990
Ngọ = 100
Ap =10
và 0=5
=>1990+100+10+5=2015
Vậy 4 số cần tìm như trên