Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
TXĐ: $[0;2]$. Hàm nghịch biến khi \(y'=\frac{1-x}{\sqrt{2x-x^2}}<0\Leftrightarrow \left\{\begin{matrix} 1-x< 0\\ 2x-x^2>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x>1\\ 0< x< 2\end{matrix}\right.\)
$\Leftrightarrow 1< x< 2$
Đáp án C.

\(y'=-3x^2+6x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
Hàm đồng biến trên \(\left(0;2\right)\)

\(f'\left(x\right)=\left(x-1\right)\left(x+1\right)\left(x+1\right)\left(x-2\right)=\left(x+1\right)^2\left(x-1\right)\left(x-2\right)\)
\(f'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\) (chỉ quan tâm nghiệm bội lẻ)
\(g'\left(x\right)=\left(1-2x\right)f'\left(x-x^2\right)=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\f'\left(x-x^2\right)=0\end{matrix}\right.\)
\(f'\left(x-x^2\right)=0\Rightarrow\left[{}\begin{matrix}x-x^2=1\\x-x^2=2\end{matrix}\right.\) (đều vô nghiệm)
\(\Rightarrow g\left(x\right)\) đồng biến khi \(x< \dfrac{1}{2}\) và nghịch biến khi \(x>\dfrac{1}{2}\)
\(\Rightarrow C\) đúng (do \(\left(-\infty;-1\right)\subset\left(-\infty;\dfrac{1}{2}\right)\)
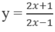 và đường thẳng y = x + 2 là:
và đường thẳng y = x + 2 là: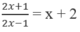
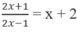
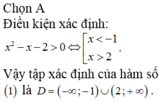
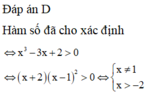

Chọn D
Điều kiện xác định của hàm số là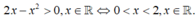
Vậy tập xác định của hàm số là D = (0;2)