AT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
H
0
H
1
23 tháng 7 2016
Áp dụng định lý Py-ta-go vào tam giác ABC vuông tại A tính BC=5cm.
Theo hệ thức lượng trong tam giác vuông ABC tính AH=2,4cm.
AM là trung tuyến tam giác ABC vuông tại A nên AM=BC/2=5/2=2,5cm.
Áp dụng định lýPy-ta-go vào tam giác AHM vuông tại H tính HM=0,7cm
CM
11 tháng 4 2019
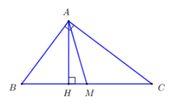
Áp dụng định lý Pytago trong tam giác vuông: ABC :
Áp dụng hệ thức lượng trong tam giác vuông ABC:
M là trung điểm củaBC
Vậy HM = BM – BH = 7 10 (cm)
Đáp án cần chọn là: A
15 tháng 5 2022
\(HC=\dfrac{3^2}{4}=2.25\left(cm\right)\)
BC=HB+HC=6,25(cm)
AM=BC/2=3,125(cm)
\(AB=\sqrt{4\cdot6.25}=5\left(cm\right)\)
\(AC=\sqrt{6.25^2-5^2}=3.75\left(cm\right)\)
15 tháng 5 2022
+ ) áp dụng định lí Pytago trong tam giác vuông \(ABH\) vuông tại \(H\) , ta có :
\(AB^2=AH^2+HB^2=3^2+4^2=25\Rightarrow AB=5\left(cm\right)\)
+ ) áp dụng hệ thức về cạnh và đường cao trong tam giác vuông \(ABC\) với \(AH\) là đường cao , ta có :
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\) \(\dfrac{1}{AC^2}=\dfrac{1}{AH^2}-\dfrac{1}{AB^2}\)
\(\Leftrightarrow\) \(\dfrac{1}{AC^2}=\dfrac{1}{3^2}-\dfrac{1}{5^2}=\dfrac{16}{225}\)
\(\Rightarrow AC=\dfrac{15}{4}\left(cm\right)\)
+ ) áp dụng định lí Pytago trong tam giác vuông \(ABC\) vuông tại \(A\) , ta có :
\(BC^2=AB^2+AC^2=5^2+\left(\dfrac{15}{4}\right)^2=\dfrac{625}{16}\)
\(\Rightarrow BC=\dfrac{25}{4}\left(cm\right)\)
+ ) tam giác \(ABC\) vuông tại \(A\) có trung tuyến \(AM\) nên ta có :
\(AM=\dfrac{1}{2}BC=\dfrac{25}{8}\left(cm\right)\)
CM
11 tháng 2 2018
+) Áp dụng định lý Pytago trong tam giác vuông ABH vuông tại H ta có:
+) Áp dụng hệ thức về cạnh và đường cao trng tam giác vuông ABC với AH là đường cao ta có:
+) Áp dụng định lý Pytago trong tam giác vuông ABC vuông tại A ta có:
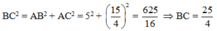
+) Tam giác ABC vuông tại A có trung tuyến AM nên ta có:
+) Diện tích tam giác ABC với AH là đường cao ta có:
Vậy AB = 5cm, AC = 15 4 cm; AM = 25 8 cm; S ∆ A B C = 75 8 c m 2 .
Đáp án cần chọn là: A
11 tháng 9 2016
BH = 18 cm ; MH = 7 cm ; MC = 25 cm ; AH = 24 cm. Chỉ có đáp án thôi nha!
14 tháng 10 2021
a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
hay AH=2,4(cm)
Xét tứ giác AMHN có
\(\widehat{MAN}=\widehat{ANH}=\widehat{AMH}=90^0\)
Do đó: AMHN là hình chữ nhật
Suy ra: AH=MN=2,4(cm)
Xét tam giác ABC vuông tại A
\(BC=\sqrt{AB+AC}=\sqrt{3^2+4^2}=5\) (đ/l py - ta - go )
A/d hệ thức lượng, ta có
\(AB^2=BC.BH\)Hay \(9=5.BC\)
=> BC = 1,8
=> CH = 3,2
\(AH=\sqrt{BH.CH}=\sqrt{1,8.3,2}=2,4\)
Mà \(AM=\frac{BC}{2}\)( Do AM là trung tuyến )
Nên => AM = 2,5
Xét tam giác AHM vuông tại H ( AH là đường cao )
\(HM=\sqrt{AM^2-AH^2}=\sqrt{2,5^2-2,4^2}=0,7\)
Vậy .....