Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Do tam giác GBC vuông tại G nên GB2 + GC2 = BC2
hay ![]()
Mặt khác theo công thức đường trung tuyến ta có
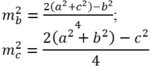
Suy ra ![]()
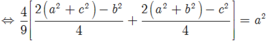
Suy ra: 4a2 + b2 + c2 = 9a2 hay
5a2 = b2 + c2.


Hình bình hành ABCD có hai đường chéo bằng nhau, nên nó là hình chữ nhật, tức là tam giác ABC vuông.
Chọn A.

Nếu G là trong tâm tam giác ABC thì
G A → + G B → + G C → = 0 → ⇔ A G → + B G → + C G → = 0 → ⇔ A G → + B G → + C G → = 0 → = 0
Đáp án C

2 M A → + M B → = C A → ⇔ 2 M A → + M B → = C M → + M A → .
⇔ M A → + M B → = − M C → ⇔ M A → + M B → + M C → = 0 → . (*)
Đẳng thức (*) suy ra M là trọng tâm của tam giác ABC.
Chọn D.

Đáp án: D
a sai vì nếu tam giác ABC thỏa mãn AB2 + AC2 = BC2 thì tam giác ABC vuông tại A không phải vuông tại B.
b, c, d đúng.

a.
Gọi (D):y=ax+b chứa điểm A, C
(D'):y=a'x+b' chứa điểm B, C
* Ta có: A thuộc (D) khi 1= 2a+b (1)
C thuộc (D) khi 4= 3a+b (2)
Giải hệ (1), (2) ta suy ra a=3 , b=-5
* Ta có: B thuộc (D') khi 3=6a'+b' (3)
C thuộc (D') khi 4=3a'+b' (4)
Giải hệ (3), (4) ta suy ra a=-1/3 , b= 5
Ta thấy: a.a' = 3.(-1/3)=-1
Suy ra (D) vuông góc (D') tại điểm chung C của của 2 cạnh (5)
Vậy tam giác ABC vuông tại C
Theo công thức tính cạnh của đoạn thẳng trong hệ trục tọa độ ta có:
AC=\(\sqrt{\left(x_A-x_C\right)^2+\left(y_A-y_C\right)^2}=\sqrt{\left(2-3\right)^2+\left(1-4\right)^2}\)\(=\sqrt{10}\)
BC=\(\sqrt{\left(x_B-x_C\right)^2+\left(y_B-y_C\right)^2}=\sqrt{\left(6-3\right)^2+\left(3-4\right)^2}\)\(=\sqrt{10}\)
Vậy AC=BC (6)
Từ (5) và (6) ta suy ra tam giác ABC vuông cân tại C
SABC=\(\dfrac{1}{2}\).AB.BC=\(\dfrac{1}{2}.\sqrt{10}.\sqrt{10}=\dfrac{1}{2}.10=\)5 (đvdt)
b. Làm tương tự câu a tìm độ dài các cạnh AB, BD, DA và tính diện tích bằng công thức SABD=\(\sqrt{p\left(p-AB\right)\left(p-BD\right)\left(p-DA\right)}\) với p là nửa chu vi tam giác ABD \(p=\dfrac{1}{2}\left(AB+BD+DA\right)\)
Tiếp tục dùng công thức SABD=\(=\dfrac{1}{2}.AB.BD.sinB\) các số liệu nêu trên đã có, chỉ cần thế vào là có góc B
Gọi I là tâm. Tìm độ dài bán kình bằng công thức SABD=\(\dfrac{AB.BD.DA}{4AI}\)
ta tìm được độ dài AI còn cách xác định tâm thì dựa vào giao điểm 2 đường thẳng (d) chứa đoạn AI và (d') chứa đoạn BI là xong

Theo hệ quả định lí cô sin trong tam giác ta có: cosB = c 2 + a 2 − b 2 2 c a
Từ giả thiết: c = a. cosB nên:
c = a . c 2 + a 2 − b 2 2. c a ⇒ c = c 2 + a 2 − b 2 2 c ⇒ 2 c 2 = c 2 + a 2 − b 2 ⇒ a 2 = b 2 + c 2
Do đó, tam giác ABC vuông tại A.
ĐÁP ÁN C