Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: BA=BM => tam giác BAM cân tại B
=> \(\widehat{AMB}=\dfrac{180-\widehat{ABC}}{2}\) (tự chứng minh) (1)
Tương tự: tam giác ANC cân tại C
=> \(\widehat{ANC}=\dfrac{180-\widehat{ACB}}{2}\) (2)
Từ 1 và 2 => \(\widehat{AMB}+\widehat{ANC}=\dfrac{180-\widehat{ABC}}{2}+\dfrac{180-\widehat{ACB}}{2}\)
\(\widehat{AMB}+\widehat{ANC}=\dfrac{180-\widehat{ABC}+180-\widehat{ACB}}{2}=\dfrac{360-90}{2}=135\)
=> MAN= 180 -135 = 45 (TỰ CHỨNG MINH)
Vậy MAN = 45
Chúc bạn hk tốt nhớ theo dõi mk vs ạ. Mk xin cảm ơn rất nhiều ạ

Ta có
BM=AB suy ra tam giác BAM cân tại B suy ra \(\widehat{BAM}=\frac{180^o-\widehat{B}}{2}\)
CN=AC suy ra tam giác NAC cân tại C suy ra \(\widehat{NAC}=\frac{180^o-\widehat{C}}{2}\)
(nếu cần thì bạn phải cm thêm cả N nằm giữa B và M nhé!)
MÀ ta thấy \(\widehat{BAM}+\widehat{ACN}=\widehat{BAC}+\widehat{NAM}\)
\(\Rightarrow\frac{180^o-\widehat{B}}{2}+\frac{180^o-\widehat{C}}{2}=90^o+\widehat{NAM}\)
\(\Rightarrow\frac{360^o-\left(\widehat{B}+\widehat{C}\right)}{2}=90^o+\widehat{NAM}\)
\(\Rightarrow\frac{360^o-90^o}{2}=90^o+\widehat{NAM}\)
\(\Rightarrow\widehat{NAM}=45^o\)
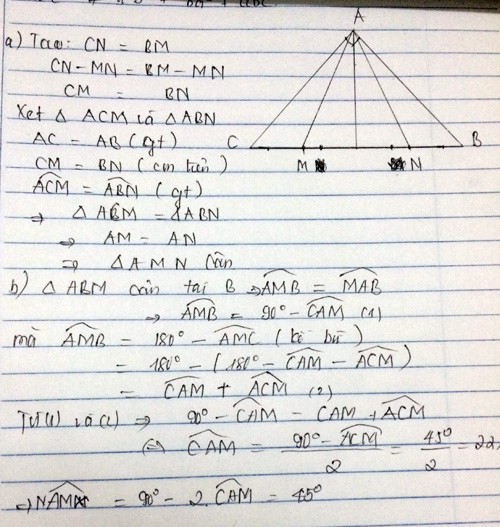
Ta có các tam giác BAM cân tại B, tam giác CAN cân tại C.
Từ đó \(\widehat{BAM}=\dfrac{180^o-\widehat{B}}{2};\widehat{CAN}=\dfrac{180^o-\widehat{C}}{2}\).
Ta có: \(\widehat{MAN}=\widehat{BAM}+\widehat{CAN}-\widehat{BAC}=\dfrac{180^o-\widehat{B}}{2}+\dfrac{180^o-\widehat{C}}{2}-90^o=\dfrac{360^o-\left(\widehat{B}+\widehat{C}\right)}{2}-90^o=\dfrac{360^o-90^o}{2}-90^o=45^o\)