Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

S A B C là hàm số của chiều cao AH.
Gọi y là diện tích của
△
ABC (
c
m
2
) và x là độ dài AH (cm) thì 
Đồ thị như hình bên.
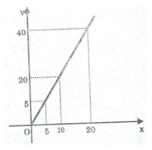

a:
| AH | 1 | 2 | 3 | 4 | 5 | 10 | 15 | 20 |
| S | 2 | 4 | 6 | 8 | 10 | 20 | 30 | 40 |
b: 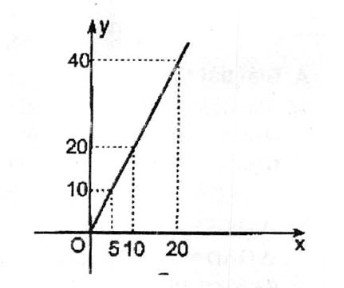
c: Diện tích tam giác tỉ lệ thuận với chiều cao

Điền vào ô trống
| Độ dài AH (cm) | 1 | 2 | 3 | 4 | 5 | 10 | 15 | 20 |
| S A B C ( c m 2 ) | 2 | 4 | 6 | 8 | 10 | 20 | 30 | 40 |

Gọi h (AH) là đường cao của \(\Delta ABC\) thì h là hằng số không đổi và cạnh đáy BC bằng a cố định .
Ta có : \(S_{ABC}=\dfrac{1}{2}BC.AH=\dfrac{1}{2}a.h\) không đổi .
Vậy diện tích tam giác ABC luôn không đồi nếu có đáy BC cố định và đỉnh A di động trên 1 đường thẳng d cố định song song với đường thẳng BC .

Đường thẳng d cố định song song với đường thẳng BC cố định nên khoảng cách hai đường thẳng d và BC là không đổi.
Tam giác ABC có cạnh đáy BC không đổi, chiều cao AH là khoảng cách giữa 2 đường thẳng song song không đổi.
Vậy điểm A thay đổi trên đường thẳng d // AB thì diện tích tam giác ABC không đổi.

Gọi h là đường cao của tam giác ABC thì h là hằng số không đổi và cạnh đấy BC = a cố định.
Ta có \(S_{ABC}=\frac{1}{2}.BC.AH=\frac{1}{2}ah\) không đổi.
Vậy có đpcm

Kẻ AK vuông góc BC. Gọi G là trọng tâm tam giác ABC và N là trung điểm BC. Kẻ GI vuông góc với AK
\(\Rightarrow\)GI // BC
\(\Rightarrow\frac{IK}{AK}=\frac{IK}{3}=\frac{GN}{AN}=\frac{1}{3}\)
\(\Rightarrow IK=1\)
Mà IK chính là khoản cách từ G đến BC
Vậy trọng tâm G nằm trên đường thẳng song song với BC và cách BC 1 khoản là 1 cm

Theo chứng minh trên, ta có:
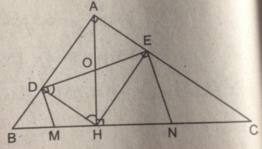
DM = MH = 1/2 BH = 1/2.4 = 2(cm)
EN = NH = 1/2 CH = 1/2.9 = 4,5(cm)
DE = AH = 6(cm)
DENM là hình thang vuông, do đó diện tích của nó là:
S D E N M = 1/2(DM + EN)DE = 1/2.(2+4,5).6 = 19,5( c m 2 ).

Tam giác ABC có đáy BC cố định, diện tích không đổi nên chiều cao AH không đổi vì thế đỉnh A chuyển động trên một đường thẳng song song với BC và cách BC một khoảng bằng h không đổi.
Vậy trọng tâm G của tam giác chạy trên đường thẳng song song BC và cách BC một khoảng h/3.
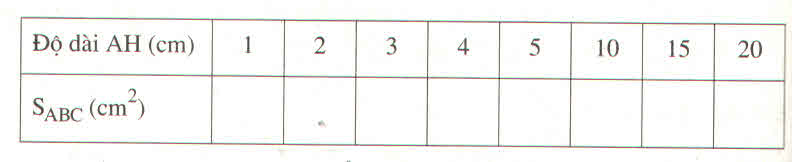

Diện tích của tam giác tỉ lệ thuận với chiều cao.