Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) _ Xét tam giác AME và tam giác AMF có :
E = F ( = 90 độ)
AM là cạnh huyền chung
A1=A2 ( AM là tia phân giác của BAC)
suy ra : tam giác AME = tam giác AMF ( CH-GN)
suy ra AE = AF ( 2 cạnh tương ứng)
suy ra tam giác AEF cân tại A
vẽ hình tạm nha
~ chúc bn học tốt~

Cậu ghi rõ ràng hơn chút được không ạ . Cậu ghi AB AC ; BE BI mình không hiểu đc

a) Xét tam giác AMB và tam giác AMC ta có:
AM là cạnh chung
AB = AC (gt)
góc BAM = góc CAM ( AM là tia phân giác của góc BAC)
=> tam giác AMB = tam giác AMC ( c - g - c)
b) Xét tam giác AEM vuông tại E và tam giác AFM vuông tại F ta có:
AM là cạnh chung
góc EAM = góc FAM ( AM là tia p/g của góc BAC)
=> tam giác AEM = tam giác AFM ( ch - gn)
=> ME = MF ( 2 cạnh tương ứng)
c) Ta có:
BI // AC (gt)
IF _|_ AC tại F (gt)
=> FI _|_ BI tại I
Ta có:
góc EBM = góc FCM ( tam giác AMB = tam giác AMC)
góc IBM = góc FCM ( 2 góc so le trong và BI // AC)
=> góc EBM = góc IBM
Xét tam giác EBM vuông tại E và tam giác IBM vuông tại I ta có:
BM là cạnh chung
góc EBM = góc IBM (cmt)
=> tam giác EBM = tam giác IBM ( ch - gn)
=> BE = BI ( 2 cạnh tương ứng)
d) Ta có:
ME = MF ( tam giác AEM = tam giác ÀM)
ME = MB ( tam giác EBM = tam giác IBM)
=> MF = MB
=> M là trung điểm của BF ( M thuộc BF)
=> MB = 1/2 IF
Mà ME = MB ( cmt)
Nên ME = 1/2 IF ( đpcm)

a) M là trung điểm của BC
=> BM=CM
tam giác ABC cân tại A
=> AB=AC
xét tam giác ABM và tam giác ACM có
AB=AC
BM=CM
cạnh AM chung
do đó : tam giác ABM= tam giác ACM ( c.c.c)
b) do tam giác ABM = tam giác ACM
=> góc A1 = góc A2
xét tam giác AEM và tam giác AFM có
cạnh AM chung
góc A1= góc A2
góc AEM=góc AFM =90 độ
do đó tam giác AEM = tam giác AFM ( cạnh huyền - góc nhọn)
c) gọi N là giao của AM va EF
do tam giác AEM= tam giác AFM
=> AE=AF
xét tam giác AEN và tam giác AFN có
cạnh AN chung
góc A1 = góc A2
AE=AF
do đó tam giác AEN=tam giác AFN ( c.g.c)
=> góc N1=góc N2
mà góc N1 + góc N2 = 180 độ ( kề bù)
=> góc N1= góc N2=90 độ
=> AN vuông góc EF
hay AM vuông góc EF
d) Qua F kẻ đg thẳng // với CE cắt AM tại H
+ HF là đg trung bình của ΔACI
⇒HF=\(\frac{1}{2}\)CI
+ ΔABM cân tại M
=> đg cao ME đồng thới là đg trung tuyến
=> AE = BE
+ Tương tự : AF = CF
+ EF là đg trung bình của ΔABC
=> EF // BC
+ Tứ giác EFCM là hbh
=> MK = FK
+ HF // CE => HF // IK
+ IK là đg trung bình của ΔMHF
\(\Rightarrow IK=\frac{1}{2}HF\Rightarrow CI=4IK\)
⇒IK=12HF⇒CI=4IK
a) M là trung điểm của BC
=> BM=CM
tam giác ABC cân tại A
=> AB=AC
xét tam giác ABM và tam giác ACM có
AB=AC
BM=CM
cạnh AM chung
do đó : tam giác ABM= tam giác ACM ( c.c.c)
b) do tam giác ABM = tam giác ACM
=> góc A1 = góc A2
xét tam giác AEM và tam giác AFM có
cạnh AM chung
góc A1= góc A2
góc AEM=góc AFM =90 độ
do đó tam giác AEM = tam giác AFM ( cạnh huyền - góc nhọn)
c) gọi N là giao của AM va EF
do tam giác AEM= tam giác AFM
=> AE=AF
xét tam giác AEN và tam giác AFN có
cạnh AN chung
góc A1 = góc A2
AE=AF
do đó tam giác AEN=tam giác AFN ( c.g.c)
=> góc N1=góc N2
mà góc N1 + góc N2 = 180 độ ( kề bù)
=> góc N1= góc N2=90 độ
=> AN vuông góc EF
hay AM vuông góc EF
hok tốt!

a) Xét \(\Delta ABM\) và \(\Delta ACM\) có:
\(AB=AC\) (do \(\Delta ABC\) cân tại \(A\))
\(\widehat{BAM}=\widehat{CAM}\) (do \(AM\) là tia phân giác \(\widehat{A}\))
\(AM\) là cạnh chung
\(\Rightarrow\Delta ABM=\Delta ACM\left(c.g.c\right)\)
b) Xét \(\Delta AEM\left(\widehat{AEM}=90^o\right)\) và \(\Delta AFM\left(\widehat{AFM}=90^o\right)\) có:
\(\widehat{EAM}=\widehat{FAM}\) (do \(AM\) là tia phân giác \(\widehat{A}\))
\(AM\) là cạnh chung
\(\Rightarrow\Delta AEM=\Delta AFM\left(ch.gn\right)\)
\(\Rightarrow AE=AF\) (\(2\) cạnh tương ứng)
\(\Rightarrow\Delta AEF\) cân tại \(A\)
c) Xét \(\Delta AEF\) cân tại \(A\) có \(AM\) là đường phân giác \(\widehat{A}\)
\(\Rightarrow AM\) cũng là đường trung trực \(\Delta AEF\)
\(\Rightarrow AM\perp EF\)
Tự vẽ hình
a, Tam giác AMB và tam giác AMC
AB = AC ( Tam giáC ABc cân )'
góc BAM = góc CAM ( AM là phân giác)
AM chung
=> Tam giác AMB = tam giác AMC ( c-g-c)
b, Xét tam giá AEM và tam giác AFM cs
góc AEM = góc AFM = 90 độ ( gt )
góc EAM = góc FAM ( AM là phân giác)
AM chung
=>tam giá AEM = tam giác AFM ( ch-gn)
=> AE = AF hay tam giác AEF cân tại A
c, Xét tam giác AEF cân tại A cs AM là tia phân giác đồng thời là đg cao
=> AM vuông góc vs EF
hình bn tự vẽ nha
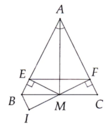
a, Xét hai tam giác vuông AME và AMF có :
AM là cạnh chung
\(\widehat{EAM} = \widehat{FAM}\) ( do AM là tia phân giác góc A )
=> tam giác AME = tam giác AMF ( cạnh huyền - góc nhọn )
=> ME = MF ( hai cạnh tương ứng )
b,Do AC // BM
mà IF vuông góc CA
=> FI vuông góc với BI ( tính chất đường vuông góc )
Do ME vuông góc AB
MI vuông góc BI
=> AB // BI ( tính chất hai đường thẳng // )
Xét hai tam giác vuông MEB và MIB có
BM là cạnh chung
\(\widehat{EMB} = \widehat{MBI}\) ( hai góc so le trong )
=> tam giác MEB = tam giác MIB ( cạnh huyền - góc nhọn )
=> BE = Bi ( hai cạnh tương ứng )
Làm thêm hộ mik phần d, tam giác BME= tam giác CMF