K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

26 tháng 2 2020
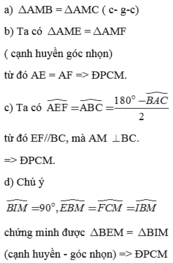
A B C M I E F
a) _ Xét tam giác AME và tam giác AMF có :
E = F ( = 90 độ)
AM là cạnh huyền chung
A1=A2 ( AM là tia phân giác của BAC)
suy ra : tam giác AME = tam giác AMF ( CH-GN)
suy ra AE = AF ( 2 cạnh tương ứng)
suy ra tam giác AEF cân tại A
vẽ hình tạm nha
~ chúc bn học tốt~
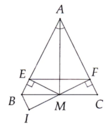
a) Xét \(\Delta ABM\) và \(\Delta ACM\) có:
\(AB=AC\) (do \(\Delta ABC\) cân tại \(A\))
\(\widehat{BAM}=\widehat{CAM}\) (do \(AM\) là tia phân giác \(\widehat{A}\))
\(AM\) là cạnh chung
\(\Rightarrow\Delta ABM=\Delta ACM\left(c.g.c\right)\)
b) Xét \(\Delta AEM\left(\widehat{AEM}=90^o\right)\) và \(\Delta AFM\left(\widehat{AFM}=90^o\right)\) có:
\(\widehat{EAM}=\widehat{FAM}\) (do \(AM\) là tia phân giác \(\widehat{A}\))
\(AM\) là cạnh chung
\(\Rightarrow\Delta AEM=\Delta AFM\left(ch.gn\right)\)
\(\Rightarrow AE=AF\) (\(2\) cạnh tương ứng)
\(\Rightarrow\Delta AEF\) cân tại \(A\)
c) Xét \(\Delta AEF\) cân tại \(A\) có \(AM\) là đường phân giác \(\widehat{A}\)
\(\Rightarrow AM\) cũng là đường trung trực \(\Delta AEF\)
\(\Rightarrow AM\perp EF\)
Tự vẽ hình
a, Tam giác AMB và tam giác AMC
AB = AC ( Tam giáC ABc cân )'
góc BAM = góc CAM ( AM là phân giác)
AM chung
=> Tam giác AMB = tam giác AMC ( c-g-c)
b, Xét tam giá AEM và tam giác AFM cs
góc AEM = góc AFM = 90 độ ( gt )
góc EAM = góc FAM ( AM là phân giác)
AM chung
=>tam giá AEM = tam giác AFM ( ch-gn)
=> AE = AF hay tam giác AEF cân tại A
c, Xét tam giác AEF cân tại A cs AM là tia phân giác đồng thời là đg cao
=> AM vuông góc vs EF