Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Có : AB=AC(tg ABC cân tại A)
BD=CE(gt)
=> AB+BD=AC+CE
=> AD=AE
=> Tg ADE cân tại A
\(\Rightarrow\widehat{D}=\widehat{E}=\frac{180^o-\widehat{A}}{2}\)
Lại có : \(\widehat{ABC}=\widehat{ACB}=\frac{180^o-\widehat{A}}{2}\)(tg ABC cân tại A)
\(\Rightarrow\widehat{D}=\widehat{ABC}=\frac{180^o-\widehat{A}}{2}\)
Mà chúng là 2 góc đồng vị
=> BC//DE
b) Có : \(\widehat{CBD}=180^o-\widehat{ABC}\)
\(\widehat{BCE}=180^o-\widehat{ACB}\)
Mà : \(\widehat{ABC}=\widehat{ACB}\)(tg ABC cân tại A)
\(\Rightarrow\widehat{CBD}=\widehat{BCE}\)
- Xét tg BCD và CBE có :
BD=CE(gt)
BC-cạnh chung
\(\widehat{CBD}=\widehat{BCE}\left(cmt\right)\)
=> Tg BCD=CBE(c.g.c)
=> BE=CD(đccm)
c) Có : \(\widehat{KBC}=\widehat{KCB}\)(tg BCD=CBE)
=> Tg KBC cân tại K
- Có : \(\widehat{KDE}=\widehat{ADE}-\widehat{ADC}\)
\(\widehat{KED}=\widehat{AED}-\widehat{AEB}\)
Mà : \(\widehat{AED}=\widehat{ADE}\)(tg ADE cân tại A)
\(\widehat{ADC}=\widehat{AEB}\)(tg BCD=CBE)
\(\Rightarrow\widehat{KED}=\widehat{KDE}\)
=> Tg KDE cân tại K
d) Xét tam giác ABK và ACK có :
AB=AC(tg ABC cân tại A)
AK-cạnh chung
KB=KC(tg KBC cân tại K)
=> Tg ABK=ACK(c.c.c)
=> \(\widehat{BAK}=\widehat{CAK}\)
=> AK là tia pg góc BAC
e) Không thấy rõ đề : DM và EN như thế nào so với BC?

\(b^2=a.c\)\(=>\frac{a}{b}=\frac{b}{c}\)
Đặt : \(\frac{a}{b}=\frac{b}{c}=k\)
Ta có : \(a=b.k\)
\(b=c.k\)
\(=>\)\(\frac{a}{c}=\frac{b.k}{c}=\frac{c.k+k}{c}=k^2\left(1\right)\)
\(\left(\frac{a+2012b}{b+2012c}\right)^2=\left(\frac{bk+2012b}{ck+2012c}\right)^2=\left(\frac{b\left(k+2012\right)}{c\left(k+2012\right)}\right)^2=\left(\frac{b}{c}\right)^2=k^2\left(2\right)\)
Từ (1) và (2) \(=>\frac{a}{c}=\left(\frac{a+2012b}{b+2012c}\right)^2\left(đpcm\right)\)
Hok tốt~

Theo đề bài, x và y là hai đại lượng tỉ lệ thuận nên y = kx
Mà khi x =-1 thì y = 2 nên 2 = k.(-1) ⇒⇒ k = -2
Ta điền vào bảng sau:
|
x |
-2 |
-1 |
1 |
3 |
4 |
|
y |
4 |
2 |
-2 |
-6 |
-8 |
x và y tỉ lệ thuận nên y = k.x
Từ đó ta tìm được y lần lượt là:
(-2).(-3) = 6 ; (-2) (-1) = 2;
(-2).1 = (-2) ; (-2).5 = -10
Ta được bảng sau
| x | -3 | -1 | 1 | 2 | 5 |
| y | 6 | 2 | -2 | -4 | -10 |

a)\(\Delta ABH\) vuông tại H có:
BH2 =AB2 -AH2 =132 -122 =25( ĐL Pytago)
=> BH=5 cm
BC=BH+HC=5+16=21 cm
\(\Delta AHC\) vuông tại H có:
AH2 + HC2 =AC2 ( đl Pytago)
=> AC2 =122 + 162 =20 cm
b) \(\Delta AHB\) vuông tại H có: AB2 = AH2 +BH2 ( ĐL Pytago)
=> BH2 =AB2 - AH2 =132 - 122 =25
=> BH=5 cm
BC= BH+HC=5+16=21 cm
\(\Delta AHC\) vuông tại H có: AC2 = AH2 +HC2 ( đL Pytago)
=> AC2 = 122 + 162 =400
=> AC= 20 cm

a) Điền số thích hợp vào ô trống:
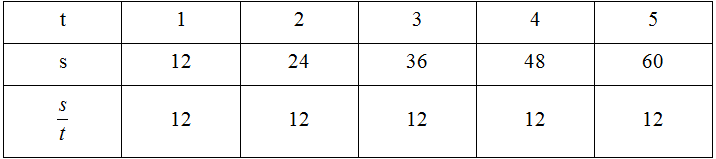
b) Hai đại lượng s và t tỉ lệ thuận vì s =12t, hệ số tỉ lệ bằng 12.

Answer:
a) Với \(x=1\Rightarrow y=2\)
\(\Rightarrow\) Điểm \(A\left(1;2\right)\in\) đồ thị hàm số \(\left(d\right)\)
Vậy hai điểm \(O\left(0;0\right);A\left(1;2\right)\) là đồ thị hàm số \(\left(d\right)\)
(Vì phần này tự nhiên không gửi được hình nên là nếu bạn có nhu cầu hình nữa thì nhắn cho mình nhé.)
b) Ta thay \(x=x_P=40\) vào \(\left(d\right)\)
Có: \(y=2.40=80\ne y_P\)
\(\Rightarrow\) Điểm \(P\left(40;20\right)\in\) đồ thị hàm số \(\left(d\right)\)
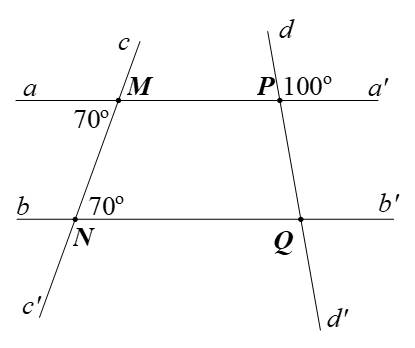
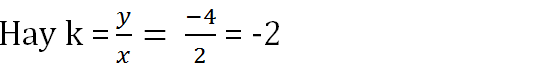
a: Vì góc aMN=góc MNQ
nên aa'//bb'
b: góc PQN=180-100=80 độ=góc b'Qd'
góc b'Qd=d'QN=180-80=100 độ