Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án cần chọn là: D
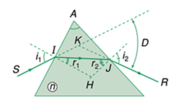
sin i 1 = n sin r 1 ; sin i 2 = n sin r
r 1 + r 2 = A
D = i 1 + i 2 − A
+ Khi góc lệch cực tiểu: sin D m + A 2 = n sin A 2
=>A, B, C đều đúng
D – sai vì: A = r 1 + r 2

Đáp án cần chọn là: D
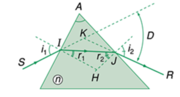
sin i 1 = n sin r 1 ; sin i 2 = n sin r
r 1 + r 2 = A
D = i 1 + i 2 − A
+ Khi góc lệch cực tiểu: sin D m + A 2 = n sin A 2
Ta suy ra các phương án: A, B, C – sai
Phương án D - đúng

Đáp án cần chọn là: D
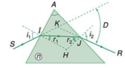
sin i 1 = n sin r 1 ; sin i 2 = n sin r 2
r 1 + r 2 = A
D = i 1 + i 2 − A
+ Khi góc lệch cực tiểu sin D m + A 2 = n sin A 2
=> A, B, Cđều đúng

Đáp án cần chọn là: A
Vì chiếu tia tới vuông góc với mặt nên i 1 = 0 → r 1 = 0
Ta có: A = r 1 + r 2 → A = r 2
Mà: D = i 1 + i 2 − A ↔ 15 = 0 + i 2 − A → i 2 = 15 + A
Lại có:
sin i 2 = n sinr 2 ↔ sin i 2 = n sin A ↔ sin ( 15 + A ) = 1,5 sin A
↔ sin 15 c osA + sinAcos 15 = 1,5 sin A
↔ sin 15 c osA = ( 1,5 − cos 15 ) sinA
→ tan A = sin 15 1,5 − c os 15 = 0,485 → A = 25,87

a) Góc lệch có giá trị cực tiểu khi: 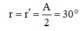
Áp dụng định luật khúc xạ ánh sáng ta có:



Chọn C
Hướng dẫn: Áp dụng công thức sin D min + A 2 = n . sin A 2 với A = 600 và n = 3 , ta được D m i n = 60 0

Đáp án cần chọn là: A
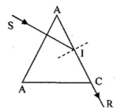
+ Vì chiếu tia tới vuông góc với mặt AB nên i 1 = 0 ⇒ r 1 = 0
+ Ta có, góc chiết quang A = r 1 + r 2 = 0 + r 2 ⇒ A = r 2
+ Vì tia ló đi là là mặt AC nên i 2 = 90 0
Áp dụng định luật khúc xạ ánh sáng tại mặt AC, ta có:
sin i 2 = n sin r 2
⇔ sin 90 0 = 2 sinr 2
⇒ sinr 2 = 1 2 ⇒ r 2 = 45 0
=> Góc chiết quang của lăng kính A = r 2 = 45 0

Đáp án cần chọn là: A
A - đúng vì D = i 1 + i 2 − ( r 1 + r 2 ) = i 1 + i 2 − A
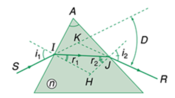
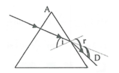
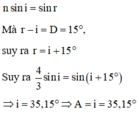
Đáp án cần chọn là: A
sin i 1 = n sin r 1 ; sin i 2 = n sin r 2
r 1 + r 2 = A
D = i 1 + i 2 − A
Khi góc lệch cực tiểu: sin D m + A 2 = n sin A 2
=> A - sai