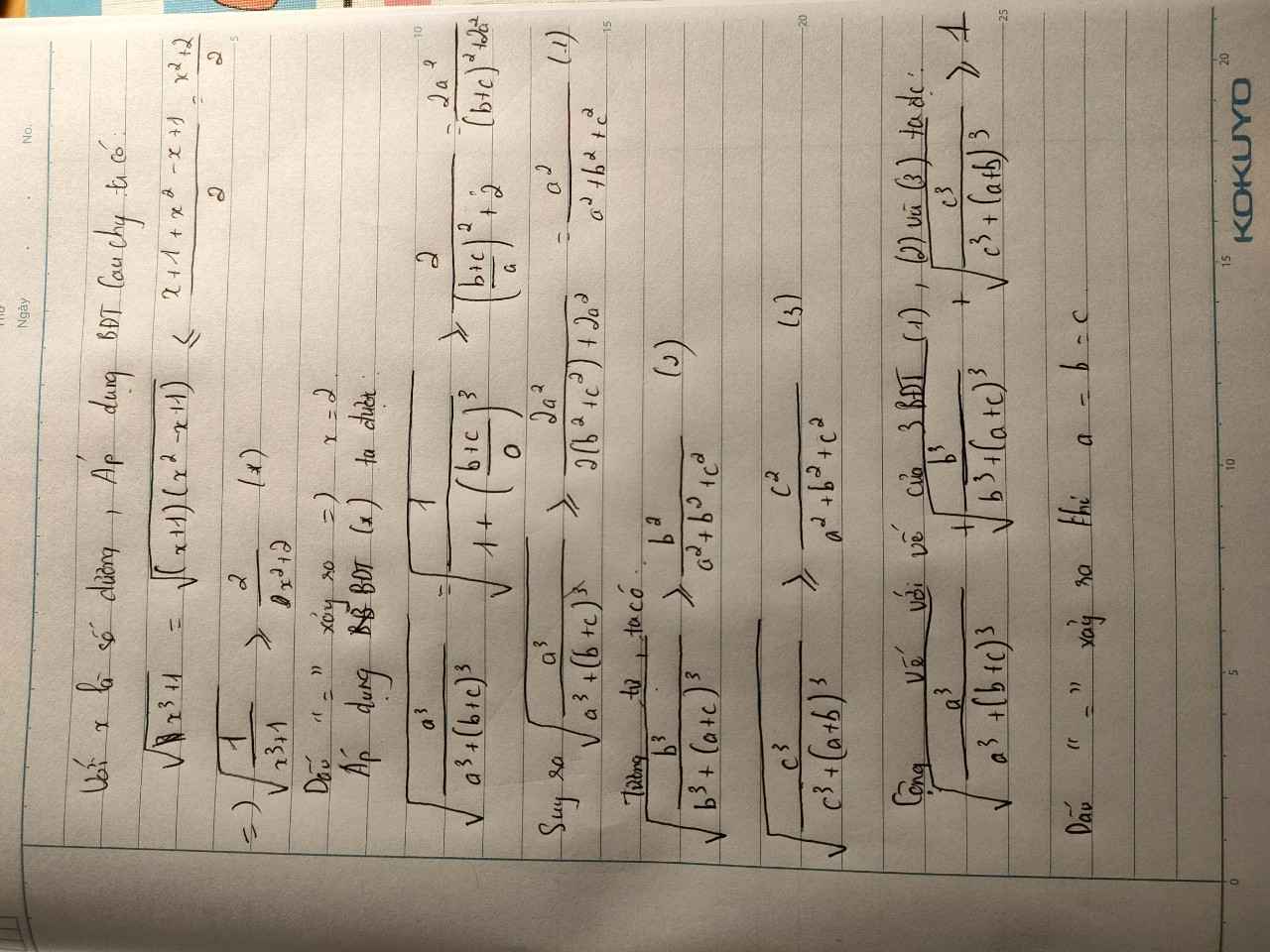Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bn tham khảo nha
https://hoc24.vn/cau-hoi/cho-ba-so-thuc-abc-duong-chung-minh-rangsqrtdfraca3a3leftbcright3sqrtdfracb3b3leftcaright3sqrtdfracc3c.5222680437292

Áp dụng BĐT: \(\left(a+b+c\right)^2\ge3\left(ab+bc+ca\right)\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\left(\text{luôn đúng}\right)\)
Ta có \(\dfrac{a}{a+1}+\dfrac{b}{b+1}+\dfrac{c}{c+1}\ge3\sqrt[3]{\dfrac{abc}{\left(a+1\right)\left(b+1\right)\left(c+1\right)}}\)
\(\dfrac{1}{a+1}+\dfrac{1}{b+1}+\dfrac{1}{c+1}\ge3\sqrt[3]{\dfrac{1}{\left(a+1\right)\left(b+1\right)\left(c+1\right)}}\)
Cộng VTV \(\Leftrightarrow3\ge\dfrac{3\left(\sqrt[3]{abc}+1\right)}{\sqrt[3]{\left(a+1\right)\left(b+1\right)\left(c+1\right)}}\Leftrightarrow\left(a+1\right)\left(b+1\right)\left(c+1\right)\ge\sqrt[3]{abc}+1\)
\(\Leftrightarrow VT^2=\sum\left[\dfrac{1}{a\left(b+1\right)}\right]^2\ge3\cdot\sum\dfrac{1}{ab\left(a+1\right)\left(b+1\right)}\\ \Leftrightarrow VT^2\ge3\cdot\dfrac{a^2+b^2+c^2+a+b+c}{abc\left(a+1\right)\left(b+1\right)\left(c+1\right)}\ge3\cdot\dfrac{a+b+c+ab+bc+ca}{abc\left(a+1\right)\left(b+1\right)\left(c+1\right)}\\ \Leftrightarrow VT^2\ge\dfrac{3}{abc}-\dfrac{3\left(abc+1\right)}{abc\left(a+1\right)\left(b+1\right)\left(c+1\right)}\ge\dfrac{3}{abc}-\dfrac{3\left(abc+1\right)}{abc\left(1+\sqrt[3]{abc}\right)^3}\\ \Leftrightarrow VT^2\ge\dfrac{9}{\sqrt[3]{\left(abc\right)^2}\left(1+\sqrt[3]{abc}\right)^2}=VP^2\\ \LeftrightarrowĐpcm\)
Dấu \("="\Leftrightarrow a=b=c=1\)

\(\dfrac{9\sqrt{5}+3\sqrt{27}}{\sqrt{5}+\sqrt{3}}=\dfrac{9\sqrt{5}+9\sqrt{3}}{\sqrt{5}+\sqrt{3}}=\dfrac{9\left(\sqrt{5}+\sqrt{3}\right)}{\sqrt{5}+\sqrt{3}}=9\)
b.
\(=\sqrt{3-\sqrt{5}}.\sqrt{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}+\sqrt{3+\sqrt{5}}.\sqrt{\left(3+\sqrt{5}\right)\left(3-\sqrt{5}\right)}\)
\(=\sqrt{3-\sqrt{5}}.\sqrt{9-5}+\sqrt{3+\sqrt{5}}.\sqrt{9-5}\)
\(=\sqrt{12-4\sqrt{5}}+\sqrt{12+4\sqrt{5}}\)
\(=\sqrt{\left(\sqrt{10}-\sqrt{2}\right)^2}+\sqrt{\left(\sqrt{10}+\sqrt{2}\right)^2}\)
\(=\sqrt{10}-\sqrt{2}+\sqrt{10}+\sqrt{2}=2\sqrt{10}\)
c.
\(\dfrac{a-\sqrt{b}}{\sqrt{b}}:\dfrac{\sqrt{b}}{a+\sqrt{b}}=\dfrac{\left(a-\sqrt{b}\right)\left(a+\sqrt{b}\right)}{\sqrt{b}.\sqrt{b}}=\dfrac{a^2-b}{b}\)

\(A=\left(\dfrac{\sqrt{2}\left(\sqrt{2}+1\right)}{\sqrt{2}+1}-\dfrac{\sqrt{5}\left(\sqrt{3}-\sqrt{7}\right)}{\sqrt{3}-\sqrt{7}}\right).\left(\sqrt{2}+\sqrt{5}\right)\)
\(=\left(\sqrt{2}-\sqrt{5}\right)\left(\sqrt{2}+\sqrt{5}\right)=2-5=-3\)
\(B=\dfrac{12\left(3-\sqrt{3}\right)}{\left(3+\sqrt{3}\right)\left(3-\sqrt{3}\right)}-\dfrac{2\sqrt{3}.\sqrt{3}}{\sqrt{3}}+\dfrac{3}{\sqrt{2}}-\dfrac{3}{\sqrt{3}}\)
\(=\dfrac{12\left(3-\sqrt{3}\right)}{6}-2\sqrt{3}+\dfrac{3\sqrt{2}}{2}-\sqrt{3}\)
\(=2\left(3-\sqrt{3}\right)-3\sqrt{3}+\dfrac{3\sqrt{2}}{2}=6-5\sqrt{3}+\dfrac{3\sqrt{2}}{2}\) (câu này khả năng đề sai, dấu \(\sqrt{3}.\sqrt{2}\) ở mẫu cuối cùng là dấu trừ mới hợp lý)
\(C=\left(\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right).\left(\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}-\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\right)\)
\(=\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}.\dfrac{3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}=\dfrac{3}{\sqrt{x}\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)^2}\)
Dấu giữa 2 dấu ngoặc là dấu chia sẽ hợp lý hơn

b: \(=\left(\sqrt{ab}+\dfrac{2\sqrt{ab}}{a}-\sqrt{\dfrac{a^2+1}{ab}}\right)\cdot\sqrt{ab}\)
\(=ab+\dfrac{2ab}{a}-\sqrt{a^2+1}=ab+2b-\sqrt{a^2+1}\)
c: \(=2\sqrt{6b}-6\sqrt{18}+10\sqrt{12}-\sqrt{48}\)
\(=2\sqrt{6b}-18\sqrt{2}+20\sqrt{3}-4\sqrt{3}\)
\(=2\sqrt{6n}-18\sqrt{2}+16\sqrt{3}\)
d: \(=\dfrac{\sqrt{3}\left(\sqrt{5}-\sqrt{2}\right)}{\sqrt{7}\left(\sqrt{5}-\sqrt{2}\right)}=\dfrac{\sqrt{21}}{7}\)