
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(A=2010.20092009-2009.20102010\)
\(A=2010.2009.10001-2009.2010.10001\)
\(A=0\)
\(A=2010\cdot20092009-2009\cdot20102010\)
\(A=2010\cdot2009\cdot10001-2009\cdot20102010\)
\(A=20102010\cdot2009-2009\cdot20102010\)
\(A=0\)

a ) T a c ó : 2009 2010 + 1 2010 = 2010 2011 + 1 2011 = 1
M à 1 2010 > 1 2011 n ê n 2009 2010 < 2010 2011
b ) T a c ó : − 199 200 + − 1 200 = − 200 201 + − 1 201 = − 1 M à − 1 200 < − 1 201 n ê n − 199 200 > − 200 201
c ) T a c ó : 103 107 + 4 107 = 113 117 + 4 117 = 1 M à 4 107 < 4 117 n ê n 103 107 < 113 117
d ) T a c ó : − 211 137 + − 63 137 = − 291 177 + − 63 177 = − 2 M à − 63 137 < − 63 177 n ê n − 211 137 > − 291 177

\(a,16^{19}=\left(2^4\right)^{19}=2^{76}\\ 8^{25}=\left(2^3\right)^{25}=2^{75}\)
Vì \(2^{76}>2^{75}=>16^{19}>8^{25}\)
b,\(3^{500}=\left(3^5\right)^{100}=243^{100}\)
Vì \(243^{100}>5^{100}=>3^{500}>5^{100}\)

a: 99^20=9801^10<9999^10
b: 3^500=243^100
5^300=125^300
=>3^500>5^300

a) \(5^{48}=\left(5^4\right)^{12}=625^{12}\)
\(2^{108}=\left(2^9\right)^{12}=512^{12}\)
Do \(625>512\Rightarrow625^{12}>512^{12}\) \(\Rightarrow5^{48}>2^{108}\) (1)
Lại có: \(108>105\Rightarrow2^{108}>2^{105}\) (2)
Từ (1) và (2) \(\Rightarrow5^{48}>2^{105}\)
b) \(2^{50}=\left(2^5\right)^{10}=32^{10}\)
Do \(33>32\Rightarrow33^{10}>32^{10}\)
Vậy \(33^{10}>2^{50}\)
c) Do \(513>512\Rightarrow513^{100}>512^{100}\) (1)
\(512^{100}=\left(2^9\right)^{100}=2^{900}\) \(=2^{10.90}=\left(2^{10}\right)^{90}=1024^{90}\) (2)
Do \(1024>1023\Rightarrow1024^{90}>1023^{90}\) (3)
Từ (1), (2) và (3) \(\Rightarrow513^{100}>1023^{90}\)
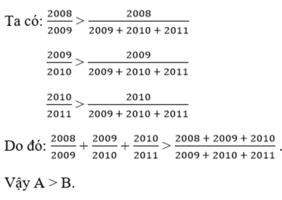
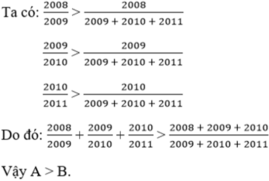
a) 85 < 3x47 b) 20092010 + 20092009 > 20102010