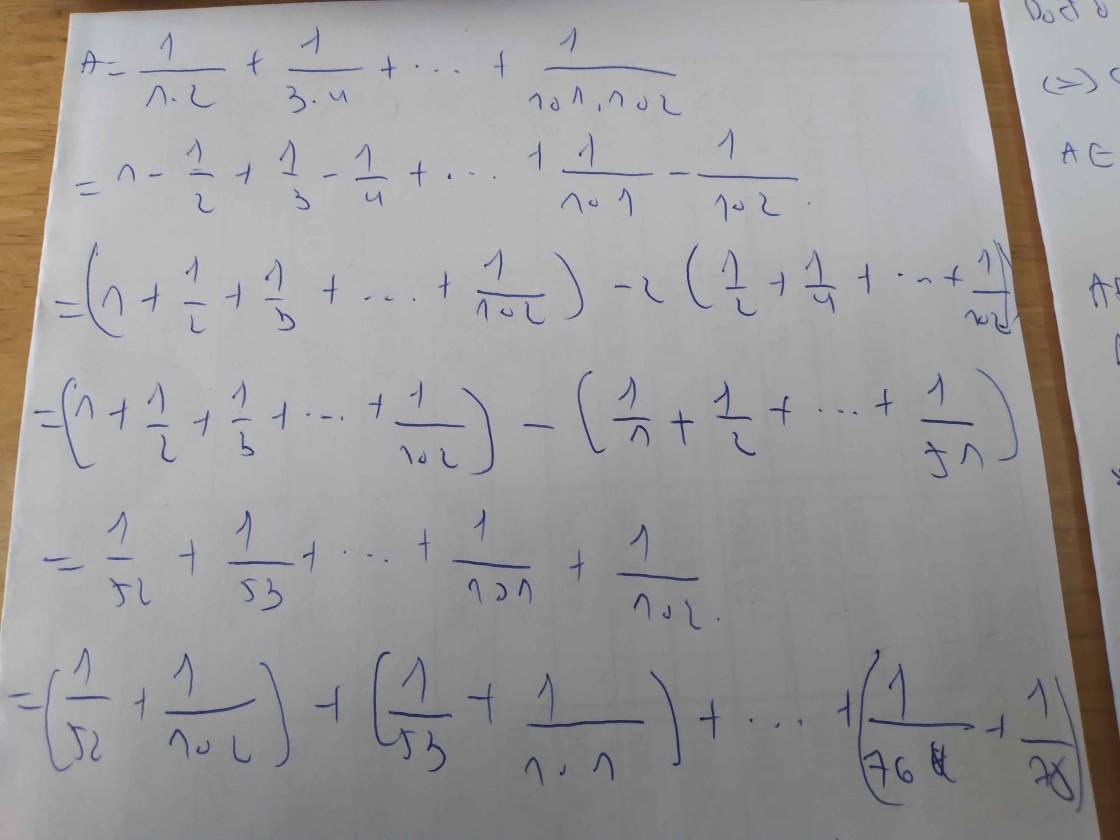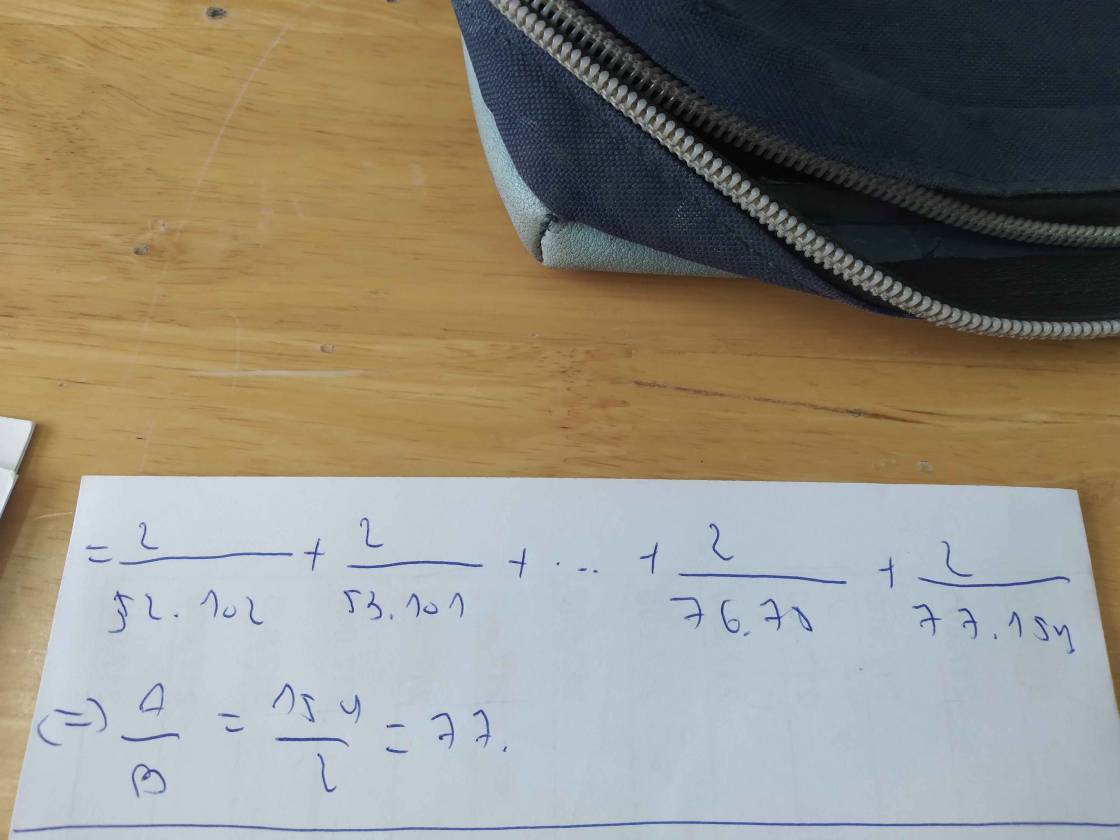Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta thấy:
\(1\cdot2^2=2^2;2\cdot3^2>3^2;3\cdot4^2>4^2;...;49\cdot50^2>50^2\)
\(\Rightarrow\dfrac{1}{1.2^2}=\dfrac{1}{2^2};\dfrac{1}{2\cdot3^2}< \dfrac{1}{3^2};\dfrac{1}{3\cdot4^2}< \dfrac{1}{4^2};...;\dfrac{1}{49\cdot50^2}< \dfrac{1}{50^2}\)
\(\Rightarrow\dfrac{1}{1\cdot2^2}+\dfrac{1}{2\cdot3^2}+\dfrac{1}{3\cdot4^2}+...+\dfrac{1}{49\cdot50^2}< \dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{50^2}\)
hay A<B
Vậy A<B

Lời giải:
Ta có:
\(\frac{1}{1.2^2}=\frac{1}{2^2}\)
\(2.3^2>3^2\Rightarrow \frac{1}{2.3^2}< \frac{1}{3^2}\)
\(3.4^2> 4^2\Rightarrow \frac{1}{3.4^2}< \frac{1}{4^2}\)
...........
\(49.50^2> 50^2\Rightarrow \frac{1}{49.50^2}< \frac{1}{50^2}\)
Cộng theo từng vế các BĐT:
\(\Rightarrow \frac{1}{1.2^2}+\frac{1}{2.3^2}+\frac{1}{3.4^2}+....+\frac{1}{49.50^2}< \frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+....+\frac{1}{50^2}\)
\(\Leftrightarrow A< B\)
Vậy ta có đpcm.

a, \(\dfrac{1}{2!}+\dfrac{2}{3!}+...+\dfrac{99}{100!}< \dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{99.100}\)
\(=\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}=1-\dfrac{1}{100}< 1\)
\(\Rightarrowđpcm\)
d, \(D=\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{99}}\)
\(\Rightarrow3D=1+\dfrac{1}{3}+...+\dfrac{1}{3^{98}}\)
\(\Rightarrow3D-D=\left(1+\dfrac{1}{3}+...+\dfrac{1}{3^{98}}\right)-\left(\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{99}}\right)\)
\(\Rightarrow2D=1-\dfrac{1}{3^{99}}\)
\(\Rightarrow D=\dfrac{1}{2}-\dfrac{1}{3^{99}.2}< \dfrac{1}{2}\)
\(\Rightarrowđpcm\)
\(\dfrac{1}{1.2}+\dfrac{1}{3.4}+...+\dfrac{1}{49.50}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{49}-\dfrac{1}{50}\)
\(=\left(1+\dfrac{1}{3}+...+\dfrac{1}{49}\right)-\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{50}\right)\)
\(=\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{49}+\dfrac{1}{50}\right)-2\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{50}\right)\)
\(=1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{49}+\dfrac{1}{50}-1-\dfrac{1}{2}-...-\dfrac{1}{25}\)
\(=\dfrac{1}{26}+\dfrac{1}{27}+...+\dfrac{1}{50}\)
\(\Rightarrowđpcm\)

a,
\(\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)+\sqrt{2}\cdot\dfrac{\sqrt{2^5}}{1-\sqrt{9}}\)
\(=2^2-\left(\sqrt{3}\right)^2+\dfrac{\sqrt{2}\cdot\sqrt{2^5}}{1-3}=4-3+\dfrac{\sqrt{2^6}}{-2}=1+\dfrac{8}{-2}=1+\left(-4\right)=-3\)
b,
\(\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{49\cdot50}\right)\cdot\dfrac{49}{50}\)
\(=\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{49}-\dfrac{1}{50}\right)\cdot\dfrac{49}{50}\)
\(=\left(1-\dfrac{1}{50}\right)\cdot\dfrac{49}{50}=\dfrac{49}{50}\cdot\dfrac{49}{50}=\dfrac{49^2}{50^2}=\dfrac{2401}{2500}\)

a) \(A=\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{100}}\)
\(2A=2\cdot\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{100}}\right)\)
\(2A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{101}}\)
\(2A-A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{99}}-\dfrac{1}{2}-\dfrac{1}{2^2}-...-\dfrac{1}{2^{100}}\)
\(A=1-\dfrac{1}{2^{100}}\)
b) \(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{2023\cdot2024}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2023}-\dfrac{1}{2024}\)
\(=1-\dfrac{1}{2024}\)
\(=\dfrac{2024}{2024}-\dfrac{1}{2024}\)
\(=\dfrac{2023}{2024}\)

Ta có A = 1 / 2 . ( 1 - 1 / 2 + 1 / 2 - 1/ 3 + ............+ 1 / 49 - 1 / 50 )
= 1/ 2 . 1 + ( -1/2 + 1/2 ) + ...........+ ( - 1/49 + 1/49 ) -1/50
=1/2 + 0 + 0 + .................+ 0 - 1/50
= 1/2 - 1/50
=12/25
Vậy A = 12/25
Ta có 12/25 < 1/2
vậy 25/12 < 1/2

2, a-b=ab => a=ab+b => a=b(a+1)
thay a=b(a+1) vào a:b ta có: => b:b(a+1)=a+1
Theo bài ra ta có: a:b=a-b
=> a+1=a-b
=>-b=1
=> b=-1
Thay b=-1 vào a-b=ab ta có : a-(-1)=-a
=> a +1=-a
=>a=-1/2
Vậy a=-1/2. b=-1

a) Ta có:
2A=2.(12+122+123+...+122020+122021)2�=2.12+122+123+...+122 020+122 021
2A=1+12+122+123+...+122019+1220202�=1+12+122+123+...+122 019+122 020
Suy ra: 2A−A=(1+12+122+123+...+122019+122020)2�−�=1+12+122+123+...+122 019+122 020
−(12+122+123+...+122020+122021)−12+122+123+...+122 020+122 021
Do đó A=1−122021<1�=1−122021<1.
Lại có B=13+14+15+1360=20+15+12+1360=6060=1�=13+14+15+1360=20+15+12+1360=6060=1.
Vậy A < B.