Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : \(11^{1979}< 11^{1980}=\left(11^3\right)^{660}=1331^{660}\)
\(37^{1320}=\left(37^2\right)^{660}=1329^{660}\)
Vì \(1329^{660}>1331^{660}\) nên \(11^{1979}< 37^{1320}\)
Bài của bạn bị nhầm chỗ này nhé: 1329660 < 1331660

202³⁰³ = (202³)¹⁰¹ = 8242408¹⁰¹
303²⁰² = (303²)¹⁰¹ = 91809¹⁰¹
Do 8242408 > 91809 nên 8282408¹⁰¹ > 91809¹⁰¹
Vậy 202³⁰³ > 303²⁰²

a, Ta có : \(8>7\)
\(\Rightarrow2^{13}.8=2^{16}>2^{13}.7\)
b, Ta có : \(199^{20}< 200^{20}=2^{60}.5^{40}\)
Mà \(2003^{15}>2000^{15}=2^{60}.2^{45}\)
Thấy : \(45>40\)
\(\Rightarrow2000^{15}>200^{20}\)
\(\Rightarrow2003^{15}>199^{20}\)
c, Ta có : \(\left\{{}\begin{matrix}202^{303}=\left(2.101\right)^{3.101}=\left(8.101^3\right)^{101}\\303^{202}=\left(3.101\right)^{2.101}=\left(9.101^2\right)^{101}\end{matrix}\right.\)
Mà \(8.101^3>9.101^2\)
\(\Rightarrow202^{303}>303^{202}\)
a) Ta có: \(2^{16}=2^{13}\cdot8\)
mà \(7< 8\)
nên \(7\cdot2^{13}< 2^{16}\)
b) \(199^{20}=1568239201^5\)
\(2003^{15}=8036054027^5\)
mà \(1568239201< 8036054027\)
nên \(199^{20}< 2003^{15}\)
c) Ta có: \(202^{303}=\left(202^3\right)^{101}\)
\(303^{202}=\left(303^2\right)^{101}\)
mà \(202^3>303^2\)
nên \(202^{303}>303^{202}\)

a) \(243^5=\left(3^5\right)^5=3^{25}\)
\(3\cdot27^5=3\cdot\left(3^3\right)^5=3\cdot3^{15}=3^{16}\)
mà \(3^{25}>3^{16}\)
nên \(243^5>3\cdot27^5\)
b) \(625^5=\left(5^4\right)^5=5^{20}\)
\(125^7=\left(5^3\right)^7=5^{21}\)
mà \(5^{20}< 5^{21}\)
nên \(625^5< 125^7\)
c) \(202^{303}=\left(202^3\right)^{101}=8242408^{101}\)
\(303^{202}=\left(303^2\right)^{101}=91809^{101}\)
mà \(8242408^{101}>91809^{101}\)
nên \(202^{303}>303^{202}\)

1 ) \(a=231.239=\left(235-4\right)\left(235+4\right)=235^2-16< 235^2=b\)
2 ) \(a=61.80=61.40.2=122.40\)
\(b=43.120=43.40.3=129.40\)
Suy ra : b > a

Bài 2:
Ta có: \(11^{1979}< 11^{1980}=1331^{660}\)
\(37^{1320}=37^{2\cdot660}=1369^{660}\)
mà \(1331^{660}< 1369^{660}\)
nên \(11^{1979}< 37^{1320}\)

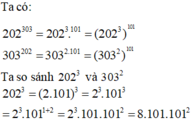
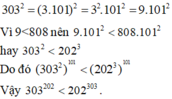
b) \(3^{21}\) và \(2^{31}\)
\(3^{21}=3.3^{20}=3.\left(3^2\right)^{10}=3.9^{10}\)
\(2^{31}=2.2^{30}=2.\left(2^3\right)^{10}=2.8^{10}\)
Vì \(3.9^{10}>2.8^{10}\)
Vậy \(3^{21}>2^{31}\)
c) \(37^{1320}\) và \(11^{1979}\)
\(37^{1320}=37^{2.660}=\left(37^2\right)^{660}=1369^{660}\)
\(11^{1979}< 11^{1980}=11^{3.660}=\left(11^3\right)^{660}=1331^{660}\)
Vì \(1369>1331\)
Nên \(1369^{660}>1331^{660}\)
Vậy \(37^{1320}>11^{1979}\)
a) \(202^{303}\) và \(303^{202}\)
\(202^{303}=202^{3.101}=\left(202^3\right)^{101}=8242408^{101}\)
\(303^{202}=303^{2.101}=\left(303^2\right)^{101}=91809^{101}\)
Vì \(8242408>91809\)
Nên \(8242408^{101}>91809^{101}\)
Vậy \(202^{303}>303^{202}\)