
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



`@` `\text {Ans}`
`\downarrow`
`a)`
\(3^{200}\text{ và }2^{300}\)
\(3^{200}=\left(3^2\right)^{100}=9^{100}\)
\(2^{300}=\left(2^3\right)^{100}=8^{100}\)
Vì `9 > 8 => 9^100 > 8^100`
`=> 3^200 > 2^300`
`b)`
\(27^{101}\text{ và }81^{35}\)
\(27^{101}=\left(3^3\right)^{101}=3^{303}\)
\(81^{35}=\left(3^4\right)^{35}=3^{140}\)
Vì `303 > 140 => 3^303 > 3^140`
`=> 27^101 > 81^35`
`c)`
\(2^{332}\text{ và }3^{223}\)
\(2^{332}< 2^{333}=\left(2^3\right)^{111}=8^{111}\)
\(3^{223}>3^{222}=\left(3^2\right)^{111}=9^{111}\)
Vì `9 > 8 => 9^111 > 8^111`
`=> 2^332 < 3^223.`
a: 3^200=9^100
2^300=8^100
mà 9>8
nên 3^200>2^300
b: 27^101=3^303
81^35=3^140
mà 303>140
nên 27^101>81^35
c: 2^332<2^333=8^111
3^223>3^222=9^111
mà 9>8
nên 3^223>8^111>2^332

1 ) Ta có : \(2^{332}< 2^{333}=\left(2^3\right)^{111}=8^{111}\)
\(2^{223}>3^{222}=\left(3^2\right)^{111}=9^{111}\)
Vì : \(8^{111}< 9^{111}\)
\(\Rightarrow2^{332}< 3^{223}\)
2 ) Ta có : \(\left(222^3\right)^{111}=\left(2.111\right)^3=8.111^3\)
\(3^{222}=\left(333^2\right)^{111}=\left(3.111\right)^2=9.111^2\)
Vì : \(8.111^2< 9.111^2\)
\(\Leftrightarrow2^{333}< 3^{222}\)
1. Ta có:
\(2^{332}< 2^{333}=\left(2^3\right)^{111}=8^{111}\)
\(3^{223}>3^{222}=\left(3^2\right)^{111}=9^{111}\)
Vì \(8^{111}< 9^{111}\) nên \(2^{332}< 8^{111}< 9^{111}< 3^{223}\Rightarrow2^{332}< 3^{223}\)
Vậy \(2^{332}< 3^{223}\)
2. Ta có:
\(2^{333}=\left(2^3\right)^{111}=8^{111}\)
\(3^{222}=\left(3^2\right)^{111}=9^{111}\)
Vì \(8^{111}< 9^{111}\) nên \(2^{333}< 3^{222}\)
Vậy \(2^{333}< 3^{222}\)

Bài này áp dụng hằng đẳng thức thứ 3 lớp 8 sẽ dễ hơn đấy ạ!
A= 2002.2004 = (2003-1).(2003+1) = 2003^2 -1. Mà B= 2003^2 => A < B

Cách 1: 92000 = (32)2000 = 34000
Vậy 92000 = 34000.
Cách 2: 34000 = (34)1000 = 811000. (1)
92000 = (92)1000 = 811000. (2)
Từ (1) và (2) suy ra 34000 = 92000 .

Ta có :
0,(41) = 0,41414141.......
0,4(14) = 0,41414141........
=> 0,(41) = 0,4(14)
Đọc xong tiện tay nhấn nút ĐÚNG hộ mình nha....moaz......moaz...

Ta có:\(2^{600}=\left(2^6\right)^{100}=64^{100}\)
\(7^{200^{ }^{ }}=\left(7^2\right)^{100}=49^{100}\)
Vì \(64^{100}>49^{100}\)
Suy ra: \(2^{600}>7^{200}\)
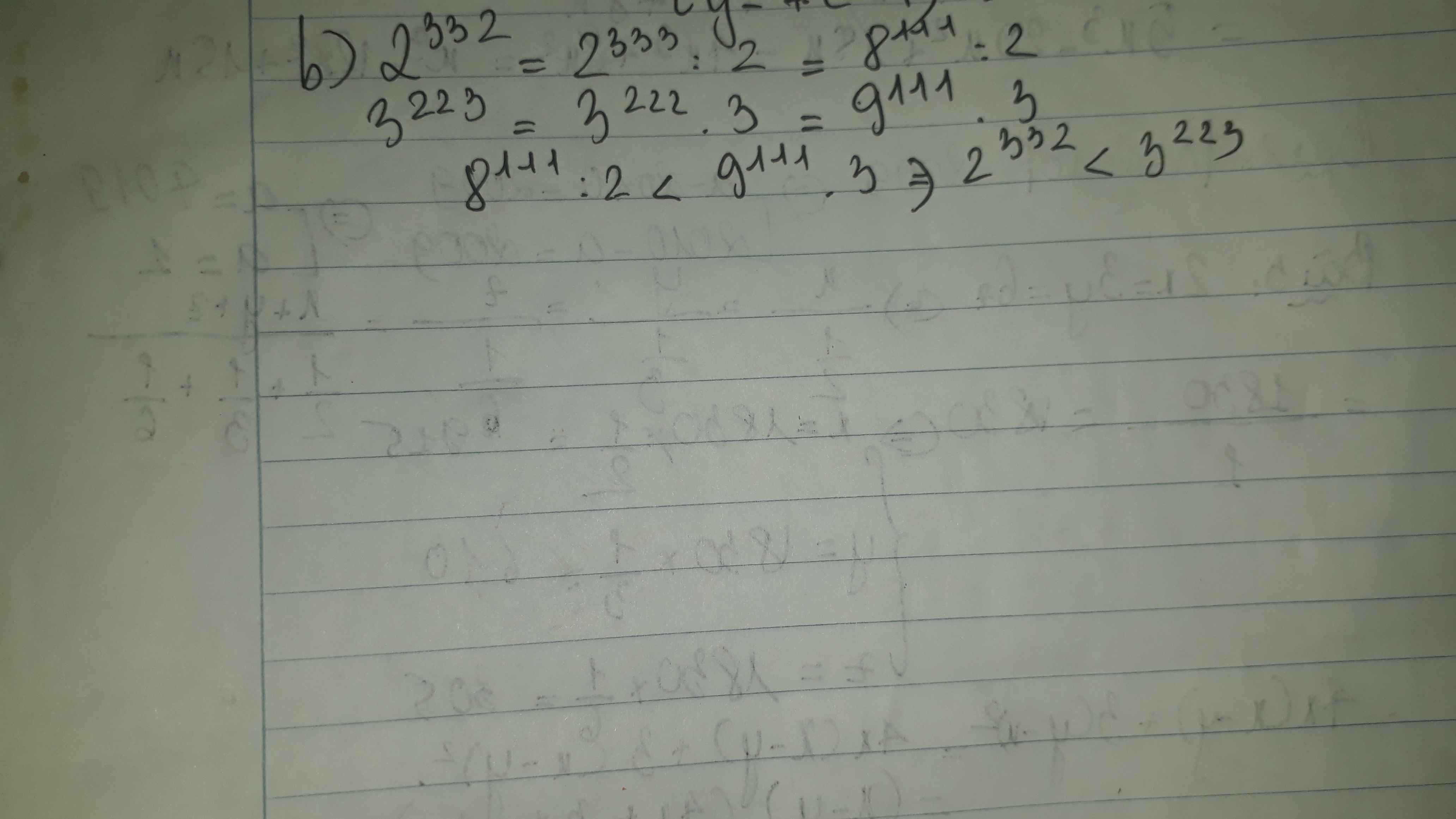

Ta có 3223 > 3222 = (32)111 = 9111. (1)
2332 < 2333 = (23)111 = 8111. (2)
Từ (1) và (2) suy ra: 2332 < 8111 < 9111 < 3223.
Vậy 2332 < 3223