
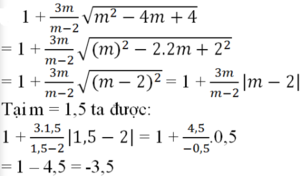
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

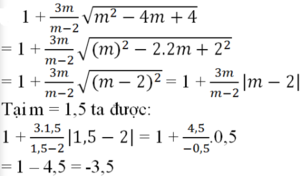

a)
Thay ta được:
.
b) Điều kiện:
+) , ta được: .
+) , ta được: .
Với . Thay vào biểu thức ta có:
Vậy giá trị biểu thức tại là .
c)
+) Với , ta được: .
+) Với , ta được: .
Vì . Thay vào biểu thức ta có: .
Vậy giá trị của biểu thức tại là .
d)
+) Với , ta có: .
+) Với , ta có: .
Vì . Thay vào biểu thức , ta có: .
Giá trị của biểu thức tại là .

a: \(M=\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{4\sqrt{x}-4}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x-4\sqrt{x}+4}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\left(\sqrt{x}-2\right)^2}{\sqrt{x}\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}-2}{\sqrt{x}}\)
b: Khi \(x=3+2\sqrt{2}=\left(\sqrt{2}+1\right)^2\) thì
\(M=\dfrac{\sqrt{\left(\sqrt{2}+1\right)^2}-2}{\sqrt{\left(\sqrt{2}+1\right)^2}}=\dfrac{\sqrt{2}+1-2}{\sqrt{2}+1}\)
\(=\dfrac{\sqrt{2}-1}{\sqrt{2}+1}=\left(\sqrt{2}-1\right)^2=3-2\sqrt{2}\)
c: M>0
=>\(\dfrac{\sqrt{x}-2}{\sqrt{x}}>0\)
mà \(\sqrt{x}>0\)
nên \(\sqrt{x}-2>0\)
=>\(\sqrt{x}>2\)
=>x>4

Tìm được A = 24 5 và B = - 6 x - 4 với x > 0 và x ≠ 4 ta tìm được 0 < x < 1
Ta có M = - 1 + 2 x ∈ Z => x ∈ Ư(2) từ đó tìm được x=1

a: \(P=\left(\dfrac{1}{m\left(m-1\right)}+\dfrac{1}{m-1}\right)\cdot\dfrac{\left(m-1\right)^2}{m+1}\)
\(=\dfrac{m+1}{m\left(m-1\right)}\cdot\dfrac{\left(m-1\right)^2}{m+1}=\dfrac{m-1}{m}\)
b: Khi m=1/2 thì \(P=\left(\dfrac{1}{2}-1\right):\dfrac{1}{2}=\dfrac{-1}{2}\cdot2=-1\)

1: \(1+\sqrt{\dfrac{\left(x-1\right)^2}{x-1}}=1+\sqrt{x-1}\)
2: \(A=\sqrt{\left(x-2\right)^2}+\dfrac{x-2}{\sqrt{\left(x-2\right)^2}}\)
=\(\left|x-2\right|+\dfrac{x-2}{\left|x-2\right|}\)
TH1: x>2
A=x-2+(x-2)/(x-2)=x-2+1=x-1
TH2: x<2
A=2-x+(x-2)/(2-x)=2-x-1=1-x
3: \(C=\sqrt{m}-\sqrt{m-2\sqrt{m}+1}\)
\(=\sqrt{m}-\sqrt{\left(\sqrt{m}-1\right)^2}\)
\(=\sqrt{m}-\left|\sqrt{m}-1\right|\)
TH1: m>=1
\(C=\sqrt{m}-\sqrt{m}+1=1\)
TH2: 0<=m<1
\(C=\sqrt{m}+\sqrt{m}-1=2\sqrt{m}-1\)

b: A=x+|x-2|
TH1: x>=2
A=x+x-2=2x-2
TH2: x<2
A=x+2-x=2
c: B=|x-3|-x
TH1: x>=3
B=x-3-x=-3
TH2: x<3
B=3-x-x=3-2x