Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1:
a: \(\dfrac{2}{5}\sqrt{75}-0,5\cdot\sqrt{48}+\sqrt{300}-\dfrac{2}{3}\cdot\sqrt{12}\)
\(=\dfrac{2}{5}\cdot5\sqrt{3}-0,5\cdot4\sqrt{3}+10\sqrt{3}-\dfrac{2}{3}\cdot2\sqrt{3}\)
\(=2\sqrt{3}-2\sqrt{3}+10\sqrt{3}-\dfrac{4}{3}\sqrt{3}\)
\(=10\sqrt{3}-\dfrac{4}{3}\sqrt{3}=\dfrac{26}{3}\sqrt{3}\)
b: \(\dfrac{9-2\sqrt{3}}{3\sqrt{6}-2\sqrt{2}}+\dfrac{3}{3+\sqrt{6}}\)
\(=\dfrac{\sqrt{3}\cdot3\sqrt{3}-2\sqrt{3}}{\sqrt{2}\left(3\sqrt{3}-2\right)}+\dfrac{3\left(3-\sqrt{6}\right)}{9-6}\)
\(=\dfrac{\sqrt{3}\left(3\sqrt{3}-2\right)}{\sqrt{2}\left(3\sqrt{3}-2\right)}+3-\sqrt{6}\)
\(=\dfrac{\sqrt{3}}{\sqrt{2}}+3-\sqrt{6}=3-\dfrac{\sqrt{6}}{2}\)
c: \(\sqrt{15-6\sqrt{6}}+\sqrt{33-12\sqrt{6}}\)
=\(\sqrt{9-2\cdot3\cdot\sqrt{6}+6}+\sqrt{24-2\cdot2\sqrt{6}\cdot3+9}\)
\(=\sqrt{\left(3-\sqrt{6}\right)^2}+\sqrt{\left(2\sqrt{6}-3\right)^2}\)
\(=\left|3-\sqrt{6}\right|+\left|2\sqrt{6}-3\right|\)
\(=3-\sqrt{6}+2\sqrt{6}-3=\sqrt{6}\)
Bài 2:
a: 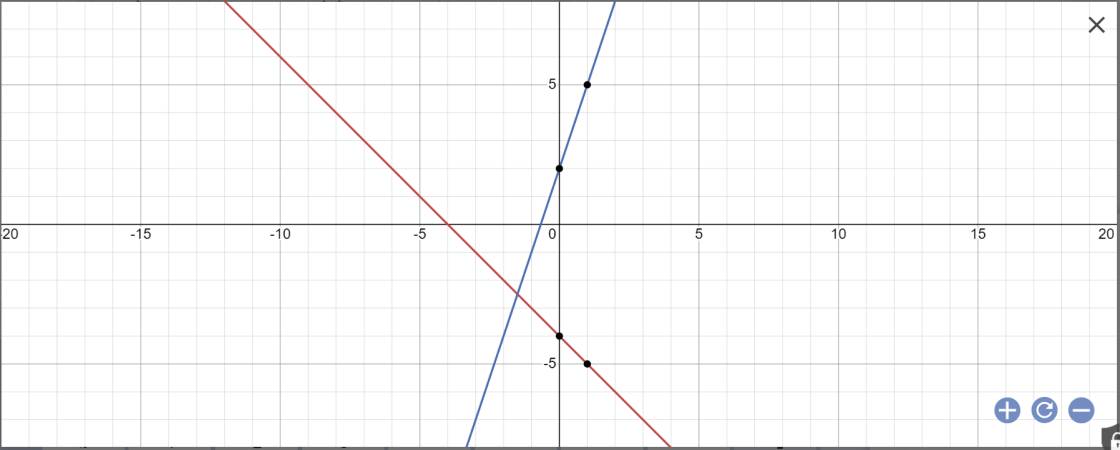
b: Phương trình hoành độ giao điểm là:
\(3x+2=-x-4\)
=>4x=-6
=>x=-3/2
Thay x=-3/2 vào y=-x-4, ta được:
\(y=-\left(-\dfrac{3}{2}\right)-4=\dfrac{3}{2}-4=-\dfrac{5}{2}\)
Vậy: \(A\left(-\dfrac{3}{2};-\dfrac{5}{2}\right)\)
c: Vì (d2)//(d) nên \(\left\{{}\begin{matrix}a=-1\\b\ne-4\end{matrix}\right.\)
Vậy: (d2): y=-x+b
Thay x=-2 và y=5 vào (d2), ta được:
\(b-\left(-2\right)=5\)
=>b+2=5
=>b=5-2=3
Vậy: (d2): y=-x+3

a) \(E=2\sqrt{40\sqrt{12}}+3\sqrt{5\sqrt{48}}-2\sqrt{\sqrt{75}}-4\sqrt{15\sqrt{27}}.\)
\(=8\sqrt{5\sqrt{3}}+6\sqrt{5\sqrt{3}}-2\sqrt{5\sqrt{3}-12\sqrt{5\sqrt{3}}}\)
\(=0\)
b) \(F=\frac{1}{\sqrt{3}}+\frac{1}{3\sqrt{2}}+\frac{1}{\sqrt{3}}\sqrt{\frac{5}{12}-\frac{1}{\sqrt{6}}}.\)
Vì \(=\frac{5}{12}-\frac{1}{\sqrt{6}}=\frac{5-2\sqrt{6}}{12}=\frac{\left(\sqrt{3}-\sqrt{2}\right)^2}{12}\)
\(\frac{1}{\sqrt{3}}+\frac{1}{2\sqrt{3}}=\frac{\sqrt{3}}{3}+\frac{\sqrt{2}}{6}=\frac{2\sqrt{3}+\sqrt{2}}{6}\)
Nên \(F=\frac{2\sqrt{3}+\sqrt{2}}{6}+\frac{1}{\sqrt{3}}\sqrt{\frac{\left(\sqrt{3}-\sqrt{2}\right)^2}{12}}=\frac{2\sqrt{3}+\sqrt{2}+\sqrt{3}-\sqrt{2}}{6}=\frac{3\sqrt{3}}{6}=\frac{\sqrt{3}}{2}\)

a: \(\dfrac{2}{\sqrt{3}-1}-\dfrac{2}{\sqrt{3}+1}\)
\(=\dfrac{2\left(\sqrt{3}+1\right)-2\left(\sqrt{3}-1\right)}{3-1}\)
\(=\dfrac{2\sqrt{3}+2-2\sqrt{3}+2}{2}=\dfrac{4}{2}=2\)
b: \(\dfrac{\sqrt{12}-\sqrt{6}}{\sqrt{30}-\sqrt{15}}\)
\(=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{\sqrt{15}\left(\sqrt{2}-1\right)}\)
\(=\dfrac{\sqrt{6}}{\sqrt{15}}=\sqrt{\dfrac{6}{15}}=\sqrt{\dfrac{2}{5}}=\dfrac{\sqrt{10}}{5}\)
c: \(\sqrt{9a}+\sqrt{81a}+3\sqrt{25a}-16\sqrt{49a}\)
\(=3\sqrt{a}+9\sqrt{a}+3\cdot5\sqrt{a}-16\cdot7\sqrt{a}\)
\(=27\sqrt{a}-112\sqrt{a}=-85\sqrt{a}\)
d: \(\dfrac{ab-bc}{\sqrt{ab}-\sqrt{bc}}=\dfrac{\left(\sqrt{ab}-\sqrt{bc}\right)\left(\sqrt{ab}+\sqrt{bc}\right)}{\sqrt{ab}-\sqrt{bc}}\)
\(=\sqrt{ab}+\sqrt{bc}\)
e: \(a\left(\sqrt{\dfrac{a}{b}+2\sqrt{ab}+b\cdot\sqrt{\dfrac{a}{b}}}\right)\cdot\sqrt{ab}\)
\(=a\cdot\sqrt{\dfrac{a}{b}\cdot ab+2\sqrt{ab}\cdot ab+b\cdot\sqrt{\dfrac{a}{b}}\cdot ab}\)
\(=a\cdot\sqrt{a^2+2\cdot ab\cdot\sqrt{ab}+a\sqrt{a}\cdot b\sqrt{b}}\)
\(=a\cdot\sqrt{a^2+3\cdot a\cdot\sqrt{a}\cdot b\cdot\sqrt{b}}\)
e: ĐKXĐ: a>=0 và a<>1
\(\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\cdot\dfrac{1+a\sqrt{a}}{1+\sqrt{a}}\)
\(=\left(\dfrac{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}+a\right)}{1-\sqrt{a}}+\sqrt{a}\right)\cdot\dfrac{\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{\sqrt{a}+1}\)
\(=\left(1+\sqrt{a}+\sqrt{a}+a\right)\cdot\left(a-\sqrt{a}+1\right)\)
\(=\left(\sqrt{a}+1\right)^2\cdot\left(a-\sqrt{a}+1\right)\)

d: \(D=\dfrac{2}{x^2-y^2}\cdot\sqrt{\dfrac{9\left(x^2+2xy+y^2\right)}{4}}\)
\(=\dfrac{2}{\left(x-y\right)\left(x+y\right)}\cdot\dfrac{3\left(x+y\right)}{2}\)
\(=\dfrac{3}{x-y}\)

a: \(=\dfrac{\sqrt{3}\left(\sqrt{5}-2\right)}{\sqrt{5}-2}-3\sqrt{3}+\dfrac{\sqrt{3}\left(\sqrt{3}+\sqrt{2}\right)}{\sqrt{3}+\sqrt{2}}\)
\(=\sqrt{3}-3\sqrt{3}+\sqrt{3}=-\sqrt{3}\)
b: \(=\left(\left(2-2\sqrt{5}\right)\left(\sqrt{5}+2\right)+\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)\)
\(=\left(2\sqrt{5}+4-10-4\sqrt{5}+\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)\)
\(=\left(-2\sqrt{5}+\sqrt{3}-6\right)\left(\sqrt{5}-\sqrt{3}\right)\)
\(=-20+2\sqrt{15}+\sqrt{15}-3-6\sqrt{5}+6\sqrt{3}\)
\(=-23+3\sqrt{15}-6\sqrt{5}+6\sqrt{3}\)

a. \(\dfrac{\sqrt{2}.\left(\sqrt{3}+\sqrt{5}\right)}{\sqrt{7}.\left(\sqrt{3}+\sqrt{5}\right)}=\dfrac{\sqrt{2}}{\sqrt{7}}=\sqrt{\dfrac{2}{7}}\)
d. \(\dfrac{\sqrt{6-2\sqrt{5}}}{\sqrt{5}-1}=\dfrac{\sqrt{5-2\sqrt{5}+1}}{\sqrt{5}-1}=\dfrac{\left(\sqrt{5}-1\right)^2}{\sqrt{5}-1}=\sqrt{5}-1\)

a: \(\sqrt{15-6\sqrt{6}}+\sqrt{33-12\sqrt{6}}\)
\(=\sqrt{9-2\cdot3\cdot\sqrt{6}+6}+\sqrt{24-2\cdot2\sqrt{6}\cdot3+9}\)
\(=\sqrt{\left(3-\sqrt{6}\right)^2}+\sqrt{\left(2\sqrt{6}-3\right)^2}\)
\(=3-\sqrt{6}+2\sqrt{6}-3=\sqrt{6}\)
b: \(\sqrt{\left(3+\sqrt{5}\right)^2}+\sqrt{14-6\sqrt{5}}\)
\(=\sqrt{\left(3+\sqrt{5}\right)^2}+\sqrt{\left(3-\sqrt{5}\right)^2}\)
\(=\left|3+\sqrt{5}\right|+\left|3-\sqrt{5}\right|\)
\(=3+\sqrt{5}+3-\sqrt{5}=6\)
c: \(\dfrac{3}{2\sqrt{3}+3}+\dfrac{3}{2\sqrt{3}-3}\)
\(=\dfrac{3\left(2\sqrt{3}-3\right)+3\left(2\sqrt{3}+3\right)}{12-9}\)
\(=2\sqrt{3}-3+2\sqrt{3}+3=4\sqrt{3}\)
d: \(\sqrt{\left(\sqrt{3}+4\right)\cdot\sqrt{19-8\sqrt{3}}+3}\)
\(=\sqrt{\left(4+\sqrt{3}\right)\cdot\sqrt{\left(4-\sqrt{3}\right)^2}+3}\)
\(=\sqrt{\left(4+\sqrt{3}\right)\cdot\left(4-\sqrt{3}\right)+3}\)
\(=\sqrt{16-3+3}=\sqrt{16}=4\)
e: \(\dfrac{9-2\sqrt{3}}{3\sqrt{6}-2\sqrt{2}}+\dfrac{3}{3+\sqrt{6}}\)
\(=\dfrac{\sqrt{3}\left(3\sqrt{3}-2\right)}{\sqrt{2}\left(3\sqrt{3}-2\right)}+\dfrac{3\left(3-\sqrt{6}\right)}{3}\)
\(=\dfrac{\sqrt{6}}{2}+3-\sqrt{6}=3-\dfrac{\sqrt{6}}{2}\)

a, \(\dfrac{2}{5}\sqrt{75}-0,5\sqrt{48}+\sqrt{300}-\dfrac{2}{3}\sqrt{12}=2\sqrt{3}-2\sqrt{3}+10\sqrt{3}-\dfrac{4}{3}\sqrt{3}=\dfrac{26}{3}\sqrt{3}\)
b, \(\dfrac{9-2\sqrt{3}}{3\sqrt{6}-2\sqrt{2}}+\dfrac{3}{3+\sqrt{6}}=\dfrac{\sqrt{3}\left(3\sqrt{3}-2\right)}{\sqrt{2}\left(3\sqrt{3}-2\right)}+\dfrac{3}{\sqrt{3}\left(\sqrt{3}+\sqrt{2}\right)}\)
\(=\dfrac{\sqrt{6}}{2}+\dfrac{\sqrt{3}}{\sqrt{3}+\sqrt{2}}\)
\(=\dfrac{\sqrt{6}}{2}+\sqrt{3}\left(\sqrt{3}-\sqrt{2}\right)\)
\(=\dfrac{\sqrt{6}}{2}+3-\sqrt{6}=\dfrac{6-\sqrt{6}}{2}\)
c, \(3\sqrt{2}-2\sqrt{3}+2\sqrt{3}+3\sqrt{2}=6\sqrt{2}\)
d, \(\sqrt{15-6\sqrt{6}}+\sqrt{33-12\sqrt{6}}=\sqrt{\left(\sqrt{6}-3\right)^2}+\sqrt{\left(2\sqrt{6}+3\right)^2}\)
\(=-\sqrt{6}+3+2\sqrt{6}+3=\sqrt{6}+6\)
e, Ghi đúng đề.
\(\dfrac{\left(\sqrt{a}-\sqrt{b}\right)^2+4\sqrt{ab}}{\sqrt{a}+\sqrt{b}}-\dfrac{a\sqrt{b}-b\sqrt{a}}{\sqrt{ab}}=\dfrac{a+b-2\sqrt{ab}+4\sqrt{ab}}{\sqrt{a}+\sqrt{b}}-\dfrac{\sqrt{ab}\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{ab}}\)
\(=\dfrac{\left(\sqrt{a}+\sqrt{b}\right)^2}{\sqrt{a}+\sqrt{b}}-\dfrac{\sqrt{ab}\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{ab}}\)
\(=\sqrt{a}+\sqrt{b}-\sqrt{a}+\sqrt{b}=2\sqrt{b}\)