
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(=\sqrt{5}-\sqrt{3}+\sqrt{5}-2=2\sqrt{5}-2-\sqrt{3}\)

\(\sqrt{12-2\sqrt{32}}+\sqrt{9+4\sqrt{2}}\)
\(=\sqrt{8-2\cdot\sqrt{8}\cdot2+4}+2\sqrt{2}+1\)
=2căn 2-2+2căn 2+1
=4căn 2-1

Đặt \(N=\sqrt{4+\sqrt{7}}-\sqrt{4-\sqrt{7}}\)
\(\Rightarrow N\sqrt{2}=\sqrt{8+2\sqrt{7}}-\sqrt{8-2\sqrt{7}}\)
\(=\sqrt{\left(\sqrt{7}+1\right)^2}-\sqrt{\left(\sqrt{7}-1\right)^2}\)
\(=\sqrt{7}+1-\sqrt{7}+1=2\)
\(\Rightarrow N=\sqrt{2}\)
\(\Rightarrow M=N-\sqrt{8}=\sqrt{2}-\sqrt{8}\)

\(=\dfrac{\sqrt{5}+1-\sqrt{5}+1}{4}=\dfrac{1}{2}\)

Ta có: \(A=\dfrac{x-4\sqrt{x}+4}{\sqrt{x}-2}+\dfrac{x+\sqrt{x}-2}{\sqrt{x}-2}\)
\(=\dfrac{2x-3\sqrt{x}+2}{\sqrt{x}-2}\)

\(\dfrac{1}{\sqrt{5}-2}+\dfrac{10}{\sqrt{5}}\)
\(=\dfrac{1\cdot\left(\sqrt{5}+2\right)}{\left(\sqrt{5}-2\right)\left(\sqrt{5}+2\right)}+\dfrac{2\sqrt{5}\cdot\sqrt{5}}{\sqrt{5}}\)
\(=\dfrac{\sqrt{5}+2}{5-2^2}+2\sqrt{5}\)
\(=\dfrac{\sqrt{5}+2}{1}+2\sqrt{5}\)
\(=\sqrt{5}+2+2\sqrt{5}\)
\(=3\sqrt{5}+2\)
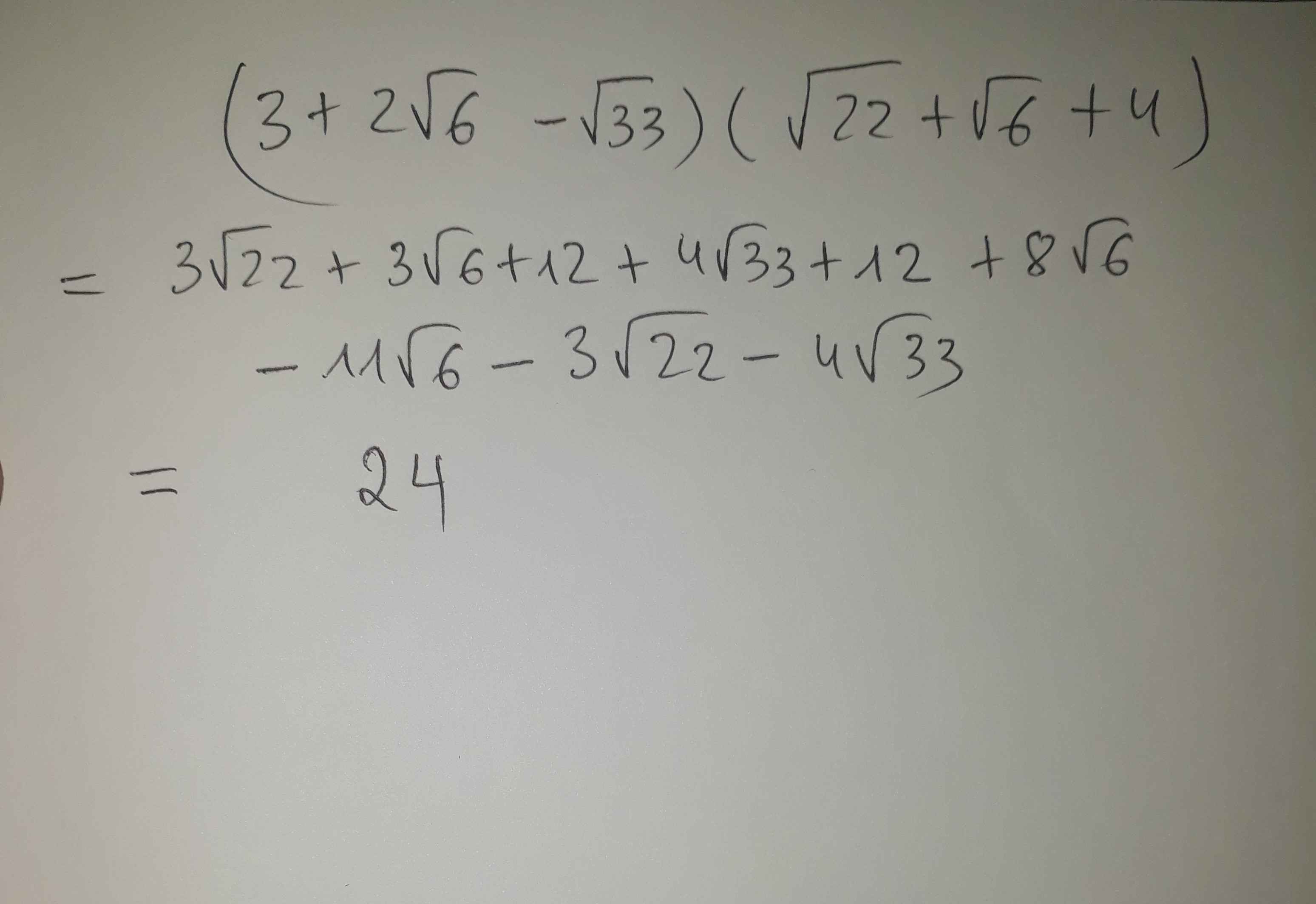
Biểu thức khai căn ra có kết quả bằng 3 nhé
bạn có thể giải ra cho mình xem được không