Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)MTC:\(12x^5y^4\)
\(\dfrac{5}{x^5y^3}=\dfrac{5\cdot12y}{x^5y^3\cdot12y}=\dfrac{60y}{12x^5y^4}\)
\(\dfrac{7}{12x^3y^4}=\dfrac{7\cdot x^2}{12x^3y^4\cdot x^2}=\dfrac{7x^2}{12x^5y^4}\)
b)MTC:\(60x^4y^5\)
\(\dfrac{4}{15x^3y^5}=\dfrac{4\cdot4x}{15x^3y^5\cdot4x}=\dfrac{16x}{60x^4y^5}\)
\(\dfrac{11}{12x^4y^2}=\dfrac{11\cdot5y^3}{12x^4y^2\cdot5y^3}=\dfrac{55y^3}{60x^4y^5}\)

\(\dfrac{5}{x^5y^3};\dfrac{7}{12x^3y^4}\)
\(MTC=12x^5y^4\)
Ta có:
\(\dfrac{5}{x^5y^3}=\dfrac{60y}{12x^5y^4}\)
\(\dfrac{7}{12x^3y^4}=\dfrac{7x^2}{12x^5y^4}\)

a) MTC: 2xy
Quy đồng: \(\frac{2x-3y}{2xy}\) giữ nguyên
\(\frac{x+2y}{x}=\frac{2y\left(x+2y\right)}{2xy}=\frac{2xy+y^2}{2xy}\)
b) \(\frac{2}{x^2-4x}=\frac{2}{x\left(x-4\right)};\frac{x}{x^2-16}=\frac{x}{\left(x-4\right)\left(x+4\right)}\)
MTC: x (x-4)(x+4)
Quy đồng : \(\frac{2}{x\left(x-4\right)}=\frac{2\left(x+4\right)}{x\left(x-4\right)\left(x+4\right)}=\frac{2x+8}{x\left(x-4\right)\left(x+4\right)}\)
\(\frac{x}{\left(x+4\right)\left(x-4\right)}=\frac{x^2}{x\left(x-4\right)\left(x+4\right)}\)
Học tốt nhé ^3^

MTC : \(150\left(x-2\right)\left(x-3\right)\)
\(\frac{5}{2x-4}=\frac{5}{2\left(x-2\right)}=\frac{5.3.\left(-25\right)\left(x-3\right)}{2.3.\left(-25\right)\left(x-2\right)\left(x-3\right)}=\frac{375\left(x-3\right)}{150\left(x-2\right)\left(x-3\right)}\)
\(\frac{z}{3x-9}=\frac{z}{3\left(x-3\right)}=\frac{z.2.\left(-25\right).\left(x-2\right)}{3.2.\left(-25\right)\left(x-3\right)\left(x-2\right)}=\frac{-50z\left(x-2\right)}{150\left(x-2\right)\left(x-3\right)}\)
\(\frac{7}{50-25x}=\frac{7}{-25\left(x-2\right)}=\frac{7.2.3.\left(x-3\right)}{-25.2.3\left(x-2\right)\left(x-3\right)}=\frac{42\left(x-3\right)}{150\left(x-2\right)\left(x-3\right)}\)


Để x;y;z ra ngoài làm thừa số chung rồi quất hết phần còn lại vào ngoặc thì thành 2 nhân tử thôi bạn, kiểu như phân phối ý.

Bài 2: \(a,\frac{7x-1}{2x^2+6x}=\frac{7x-1}{2x\left(x+3\right)}=\frac{\left(7x-1\right)\left(x-3\right)}{2x\left(x+3\right)\left(x-3\right)}\)
\(\frac{5-3x}{x^2-9}=\frac{5-3x}{\left(x-3\right)\left(x+3\right)}=\frac{\left(5-3x\right)2x}{2x\left(x-3\right)\left(x+3\right)}\)
\(b,\frac{x+1}{x-x^2}=\frac{x+1}{x\left(1-x\right)}=-\frac{x+1}{x\left(x+1\right)}=-\frac{2\left(x-1\right)\left(x+1\right)}{2x\left(x-1\right)^2}\)
\(\frac{x+2}{2-4x+2x^2}=\frac{x+2}{2\left(x-1\right)^2}=\frac{2x\left(x+2\right)}{2x\left(x-1\right)^2}\)
\(c,\frac{4x^2-3x+5}{x^3-1}=\frac{4x^2-3x+5}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(\frac{2x}{x^2+x+1}=\frac{2x\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(\frac{6}{x-1}=\frac{6\left(x^2+x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(d,\frac{7}{5x}=\frac{7.2\left(2y-x\right)\left(2y+x\right)}{2.5x\left(2y-x\right)\left(2y+x\right)}\)
\(\frac{4}{x-2y}=-\frac{4}{2y-x}=-\frac{4.2.5x\left(2x+x\right)}{2.5x\left(2y-x\right)\left(2y+x\right)}\)
\(\frac{x-y}{8y^2-2x^2}=\frac{x-y}{2\left(4y^2-x^2\right)}=\frac{x-y}{2\left(2y-x\right)\left(2y+x\right)}=\frac{5x\left(x-y\right)}{2.5x.\left(2y-x\right)\left(2y+x\right)}\)

a) MTC : \(\left(x+1\right)\left(x^2-x+1\right)\)
Quy đồng :
\(\frac{x-1}{x^3+1}=\frac{x-1}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(\frac{2x}{x^2-x+1}=\frac{2x\left(x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(\frac{2}{x+1}=\frac{2\left(x^2-x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}\)
b ) MTC : \(10x\left(2y-x\right)\left(2y+x\right)\)
\(\frac{7}{5x}=\frac{7.2.\left(2y-x\right)\left(2y+x\right)}{10x\left(2y-x\right)\left(2y+x\right)}\)
\(\frac{4}{x-2y}=\frac{-4.10x.\left(2y+x\right)}{10x\left(2y-x\right)\left(2y+x\right)}=\frac{-40x\left(2y+x\right)}{10x\left(2y-x\right)\left(2y+x\right)}\)
\(\frac{x-y}{8y^2-2x^2}=\frac{x-y}{2\left(4y^2-x^2\right)}=\frac{x-y}{2\left(2y-x\right)\left(2y+x\right)}=\frac{5x\left(x-y\right)}{10x\left(2y-x\right)\left(2y+x\right)}\)
c ) MTC : \(\left(x+2\right)^3\)
\(\frac{6x^2}{x^3+6x^2+12x+8}=\frac{6x^2}{\left(x+2\right)^3}\)
\(\frac{3x}{x^2+4x+4}=\frac{3x}{\left(x+2\right)^2}=\frac{3x\left(x+2\right)}{\left(x+2\right)^3}\)
\(\frac{2}{2x+4}=\frac{1}{x+2}=\frac{\left(x+2\right)^2}{\left(x+2\right)^3}\)

a, \(\frac{3x}{2x+4};\frac{x+3}{x^2-4}\)
Ta có : \(2x+4=2\left(x+2\right)\)
\(x^2-4=\left(x-2\right)\left(x+2\right)\)
MTC : \(2\left(x-2\right)\left(x+2\right)\)
\(\frac{3x}{2x+4}=\frac{3x}{2\left(x+2\right)}=\frac{3x\left(x-2\right)}{2\left(x-2\right)\left(x+2\right)}=\frac{3x^2-6x}{2\left(x-2\right)\left(x+2\right)}\)
\(\frac{x+3}{x^2-4}=\frac{x+3}{\left(x-2\right)\left(x+2\right)}=\frac{2x+6}{\left(x-2\right)\left(x+2\right)}\)
c, \(\frac{2x}{x^2-8x+16};\frac{x}{3x^2-12x}\)
Ta có : \(x^2-8x+16=\left(x-4\right)^2\)
\(3x^2-12x=3x\left(x-4\right)\)
MTC : \(3x\left(x-4\right)^2\)
\(\frac{2x}{x^2-8x+16}=\frac{2x}{\left(x-4\right)^2}=\frac{6x^2}{3x\left(x-4\right)^2}\)
\(\frac{x}{3x^2-12x}=\frac{x}{3x\left(x-4\right)}=\frac{x^2+4x}{3x\left(x-4\right)\left(x+4\right)}\)
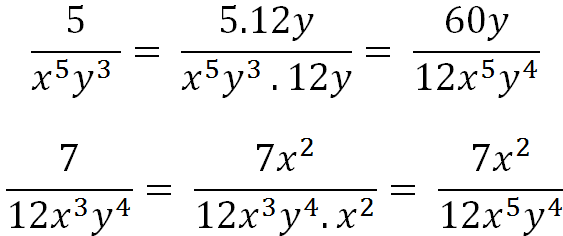
hello
kích cho tớ đi