RN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
4
HP
27 tháng 3 2021
1.
\(cosA=\dfrac{b^2+c^2-a^2}{2bc}=\dfrac{1}{2}\Rightarrow\widehat{A}=60^o\)
\(S=\dfrac{1}{2}bc.sinA=\dfrac{1}{2}.8.5.sin60^o=10\sqrt{3}\)
\(S=\dfrac{1}{2}a.h_a=\dfrac{1}{2}.7.h_a=10\sqrt{3}\Rightarrow h_a=\dfrac{20\sqrt{3}}{7}\)
\(2R=\dfrac{a}{sinA}=\dfrac{7}{\dfrac{\sqrt{3}}{2}}=\dfrac{14\sqrt{3}}{3}\Rightarrow R=\dfrac{7\sqrt{3}}{3}\)
\(S=pr=\dfrac{a+b+c}{2}.r=10r=10\sqrt{3}\Rightarrow r=\sqrt{3}\)
\(m_a^2=\dfrac{b^2+c^2}{2}-\dfrac{a^2}{4}=\dfrac{129}{4}\Rightarrow m_a=\dfrac{\sqrt{129}}{2}\)
HP
27 tháng 3 2021
6.
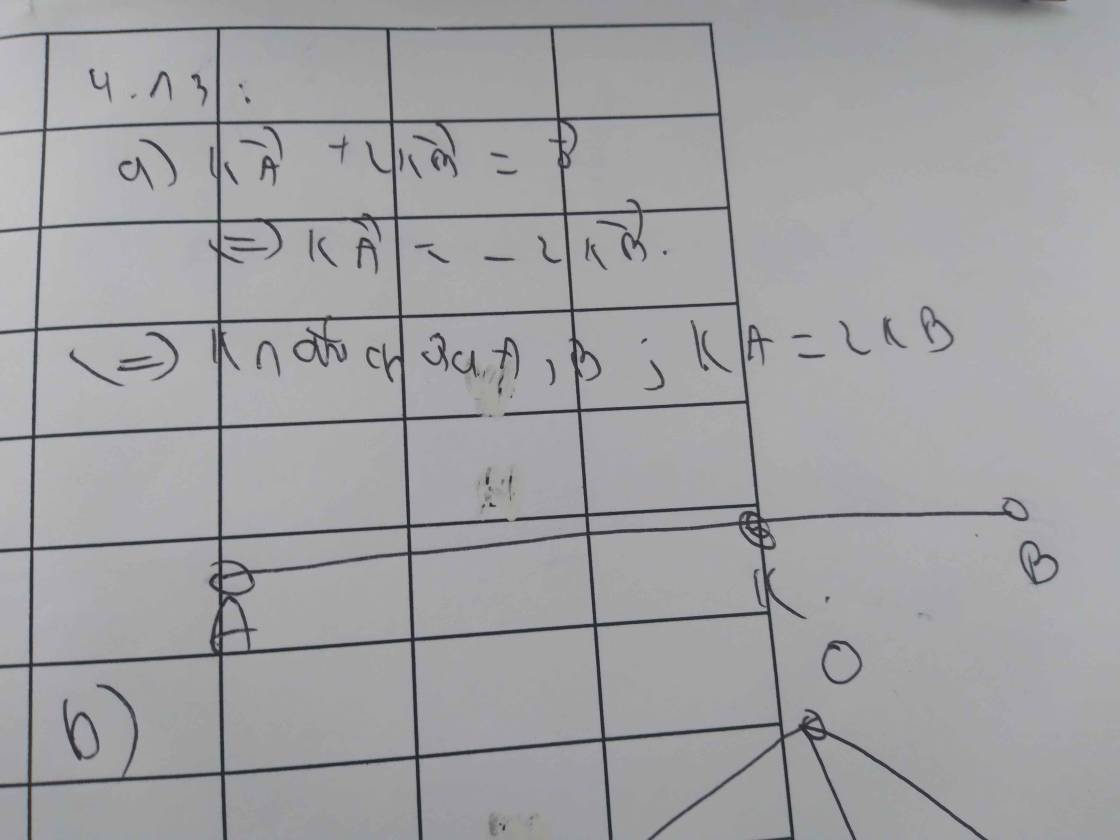
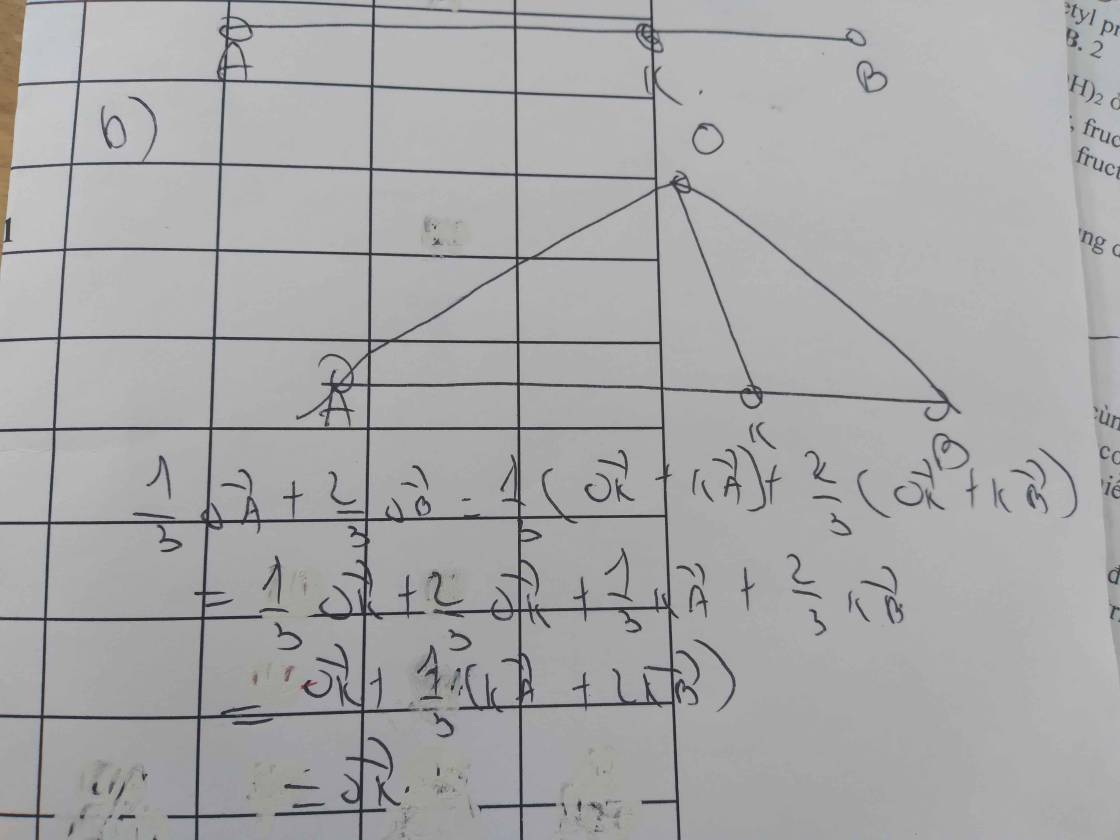
a, Công thức trung tuyến:
\(AM^2=c^2=\dfrac{b^2+c^2}{2}-\dfrac{a^2}{4}=\dfrac{2b^2+2c^2-a^2}{4}\Rightarrow a^2=2\left(b^2-c^2\right)\)
b, \(a^2=2\left(b^2-c^2\right)\Rightarrow\dfrac{2\left(b^2-c^2\right)}{a^2}=1\)
\(\Leftrightarrow2\left(\dfrac{b^2}{a^2}-\dfrac{c^2}{a^2}\right)=1\)
\(\Leftrightarrow2\left(\dfrac{b^2}{a^2}.sin^2A-\dfrac{c^2}{a^2}.sin^2A\right)=sin^2A\)
\(\Leftrightarrow2\left(sin^2B-sin^2C\right)=sin^2A\)
Hay \(sin^2A=2\left(sin^2B-sin^2C\right)\)
PK
0
5N
1
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 12 2021
ĐKXĐ: ...
\(\Leftrightarrow\sqrt{x-1}+\sqrt{x+3}+2x+2+2\sqrt{\left(x-1\right)\left(x+3\right)}-6=0\)
Đặt \(\sqrt{x-1}+\sqrt{x+3}=t>0\)
\(\Rightarrow t^2=2x+2+2\sqrt{\left(x-1\right)\left(x+3\right)}\)
Phương trình trở thành:
\(t+t^2-6=0\Rightarrow\left[{}\begin{matrix}t=2\\t=-3\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{x-1}+\sqrt{x+3}=2\)
\(\Leftrightarrow\sqrt{x-1}+\sqrt{x+3}-2=0\)
\(\Leftrightarrow\sqrt{x-1}+\dfrac{x-1}{\sqrt{x+3}+2}=0\)
\(\Leftrightarrow\sqrt{x-1}\left(1+\dfrac{\sqrt{x-1}}{\sqrt{x+3}+2}\right)=0\)
\(\Leftrightarrow\sqrt{x-1}=0\)
\(\Leftrightarrow x=1\)
LL
Làm dưới dạng tự luận ( giúp mình với ạ :< )
0
PH
1
20 tháng 11 2023
Câu 11: D
Câu 12: D
Câu 13: C
Câu 14: B
Câu 15: C
Câu 16: C
Câu 18: C
Câu 17: A
PH
1
20 tháng 11 2023
Câu 1: D
Câu 2: Những mệnh đề sai là: 2,3,4,5,7,8
=>Chọn B
Câu 3: C
Câu 4: A
Câu 5: D
Câu 6: D
Câu 7: D
Câu 8: C
Câu 9: D
Câu 10: B
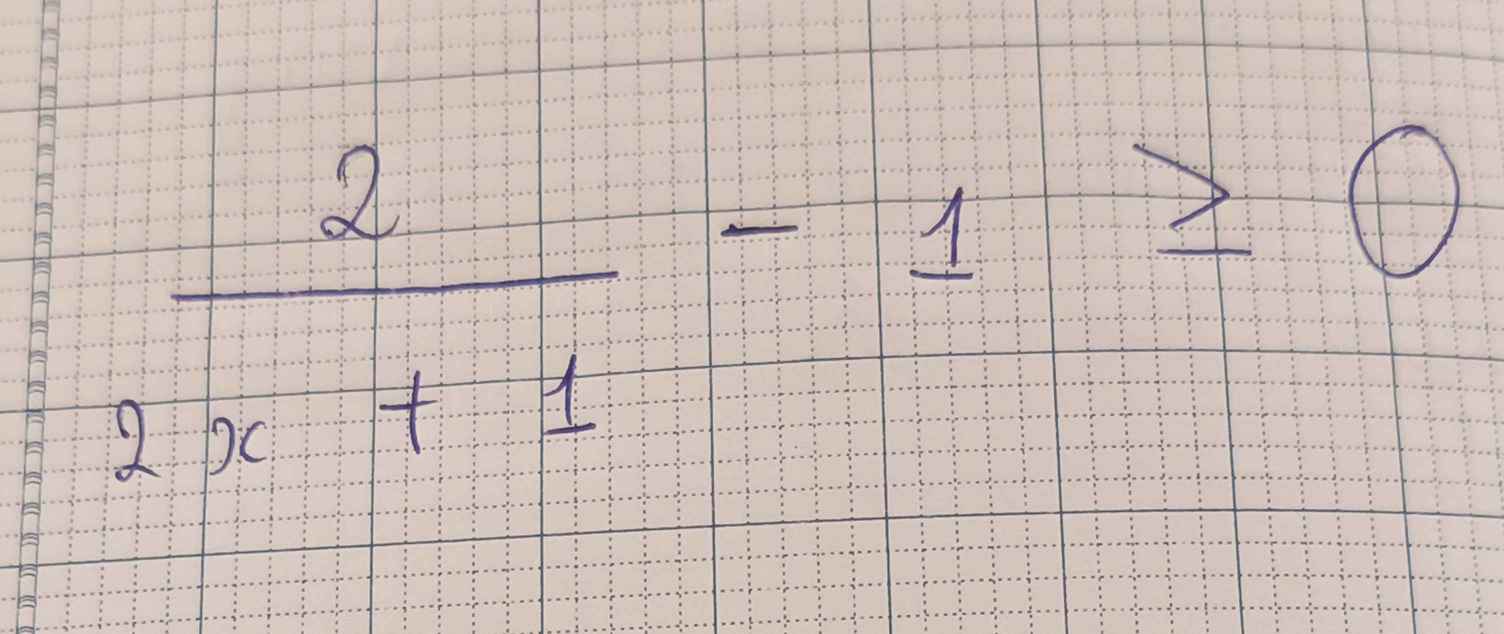
\(\dfrac{2}{2x+1}-1\ge0\Leftrightarrow\dfrac{2}{2x+1}-\dfrac{2x+1}{2x+1}\ge0\)
\(\Leftrightarrow\dfrac{2-\left(2x+1\right)}{2x+1}\ge0\)
\(\Leftrightarrow\dfrac{1-2x}{2x+1}\ge0\)
\(\Rightarrow-\dfrac{1}{2}< x\le\dfrac{1}{2}\)
Câu trả lời của cô rất hay cô ạ
Em rất cảm ơn cô vì câu trả lời này