Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

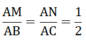
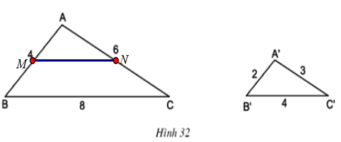
⇒ MN // BC (định lí Ta lét đảo)
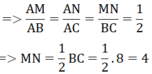
Suy ra: Δ AMN = ∆ A’B’C’(c.c.c) nên hai tam giác này cũng đồng dạng với nhau (1).
Xét tam giác ABC có MN// BC nên Δ AMN đồng dạng với tam giác ABC (2)
Từ (1) và (2) suy ra: Δ A’B’C’ đồng dạng với tam giác ABC (tính chất).

a) Vì \(MN//BC\left( {M \in AB,N \in AC} \right)\) nên \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\)(định lí Thales).
b) Vì \(AM = DE\) mà \(\frac{{DE}}{{AB}} = \frac{1}{3} \Rightarrow \frac{{AM}}{{AB}} = \frac{1}{3} \Rightarrow \frac{{AN}}{{AC}} = \frac{1}{3} \Rightarrow AN = \frac{1}{3}AC\).
Lại có \(DF = \frac{1}{3}AC\) nên \(AN = DF = \frac{1}{3}AC\).
c) Vì \(MN//BC \Rightarrow \Delta ABC\backsim\Delta AMN\) (định lí)(1)
d) Dự đoán hai tam giác \(DEF\) và \(ABC\) đồng dạng.

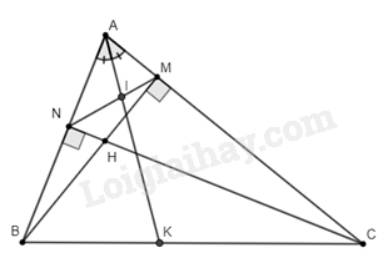
a) Vì \(BM\)là đường cao nên \(\widehat {AMB} = 90^\circ \); vì \(CN\)là đường cao nên \(\widehat {ANC} = 90^\circ \)
Xét tam giác \(AMB\) và tam giác \(ANC\) có:
\(\widehat A\) (chung)
\(\widehat {ANB} = \widehat {ANC} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta AMB\backsim\Delta ANC\) (g.g).
Suy ra, \(\frac{{AM}}{{AN}} = \frac{{AB}}{{AC}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Do đó, \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) (tỉ lệ thức)
Xét tam giác \(AMN\) và tam giác \(ABC\) có:
\(\widehat A\) (chung)
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) (chứng minh trên)
Suy ra, \(\Delta AMN\backsim\Delta ABC\) (c.g.c).
b) Xét tam giác \(AMN\) có \(AI\) là đường phân giác của \(\widehat {MAN}\left( {I \in MN} \right)\).
Theo tính chất đường phân giác ta có:
\(\frac{{IM}}{{IN}} = \frac{{AM}}{{AN}}\)
Xét tam giác \(ABC\) có \(AK\) là đường phân giác của \(\widehat {BAC}\left( {K \in BC} \right)\).
Theo tính chất đường phân giác ta có:
\(\frac{{BK}}{{KC}} = \frac{{AB}}{{AC}}\)
Mà \(\frac{{AM}}{{AN}} = \frac{{AB}}{{AC}}\) (chứng minh trên) nên \(\frac{{IM}}{{IN}} = \frac{{KB}}{{KC}}\) (điều phải chứng minh).

a) Vì tam giác \(\Delta AMN\backsim\Delta ABC\) nên ta có \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\) (các cạnh tương ứng)
Tỉ số đồng dạng là: \(\frac{{MN}}{{BC}} = \frac{4}{{12}} = \frac{1}{3}\).
b) Vì \(\Delta AMN\backsim\Delta ABC\) nên \(\widehat {AMN} = \widehat {ABC} = 65^\circ \)
Vậy \(\widehat {AMN} = 65^\circ \).
a: AM/AB=AN/AC=MN/BC=4/12=1/3
b: góc AMN=góc ABC=65 độ

Bổ sung đề: AB=6cm; AC=9cm
a: Xét ΔABC có AM/AB=AN/AC
nên MN//BC
b: Ba tam giác này đồng dạng với nhau

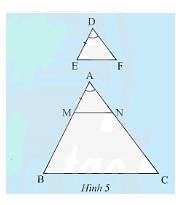
Vì \(\Delta ADE\backsim\Delta AMN\) nên \(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {ADE} = \widehat {AMN};\widehat {AED} = \widehat {ANM}\\\frac{{AD}}{{AM}} = \frac{{AE}}{{AN}} = \frac{{DE}}{{MN}}\end{array} \right.\)
Vì \(DE\) là đường trung bình của tam giác \(AMN\)nên \(DE = \frac{1}{2}MN\)
\( \Rightarrow \left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {ADE} = \widehat {AMN};\widehat {AED} = \widehat {ANM}\\\frac{{AD}}{{AM}} = \frac{{AE}}{{AN}} = \frac{{DE}}{{MN}} = \frac{1}{2}\end{array} \right.\)
\( \Rightarrow AM = 2AD;AN = 2AE;MN = 2DE\)
Lại có, \(\Delta AMN\backsim\Delta ABC\) nên \(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\\\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\end{array} \right.\)
Vì \(MN\) là đường trung bình của tam giác \(ABC\)nên \(MN = \frac{1}{2}BC\)
\(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\\\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{2}\end{array} \right.\)
\( \Rightarrow AB = 2AM;AC = 2AN;BC = 2MN\)
Vì tam giác \(\Delta ADE\backsim\Delta AMN,\Delta AMN\backsim\Delta ABC,\) nên \(\Delta ADE\backsim\Delta ABC\)
Tỉ số đồng dạng là: \(\frac{{AD}}{{AB}} = \frac{{\frac{{AM}}{2}}}{{2AM}} = \frac{1}{4}\).
Vậy tỉ số đồng dạng là \(\frac{1}{4}\).

\(BE||DM\) (cùng vuông góc AC)
Theo định lý Talet: \(\left\{{}\begin{matrix}\dfrac{MK}{EH}=\dfrac{CK}{CH}\\\dfrac{DK}{BH}=\dfrac{CK}{CH}\end{matrix}\right.\) \(\Rightarrow\dfrac{MK}{EH}=\dfrac{DK}{BH}\)
\(\Rightarrow\dfrac{BH}{EH}=\dfrac{DK}{MK}\)
Hai tam giác vuông AHE và ACD đồng dạng (chung góc A) \(\Rightarrow\dfrac{AH}{AC}=\dfrac{AE}{AD}\Rightarrow AH.AD=AC.AE\)
Tương tự CHE đồng dạng CAF \(\Rightarrow\dfrac{CH}{AC}=\dfrac{CE}{CF}\Rightarrow CH.CF=AC.CE\)
\(\Rightarrow AH.AD+CH.CF=AC.AE+AC.CE=AC\left(AE+CE\right)=AC^2\) (1)
Lại có 2 tam giác vuông ACD và DCM đồng dạng (chung góc C)
\(\Rightarrow\dfrac{AC}{CD}=\dfrac{CD}{CM}\Rightarrow AC=\dfrac{CD^2}{CM}\Rightarrow AC^2=\dfrac{CD^4}{CM^2}\) (2)
(1); (2) suy ra đpcm
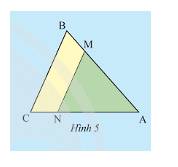

Vì \(MN//BC\) nên \(\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\) (các cặp góc đồng vị)
Xét tam giác \(ABC\) có, \(MN//BC\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\).
Vậy trong các ô trống cần điền là:
\(\widehat A\) chung;
\(\widehat M = \widehat B\);
\(\widehat N = \widehat C\);
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\).
Tam giác \(\Delta AMN\) và\(\Delta ABC\) có các góc tương ứng bằng nhau và tỉ số các cạnh tương ứng bằng nhau nên \(\Delta AMN\) đồng dạng \(\Delta ABC\).