Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

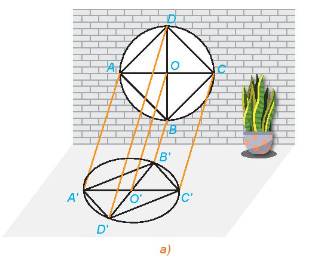
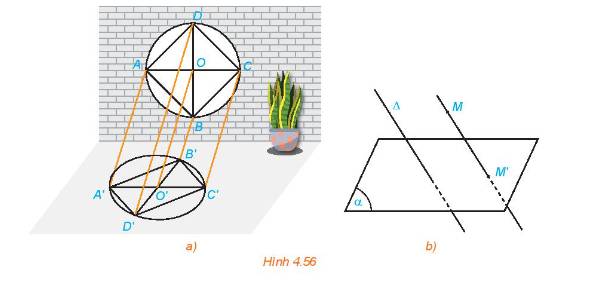
a) Các đường thẳng nối mỗi điểm A, B, C với bóng A', B', C' có đôi một song song.
b) Để xác định được bóng đổ trên sàn nhà của mỗi điểm trên khung cửa sổ ta lấy một đường thẳng a cố định song song với ánh mặt trời.
Điểm O' là giao điểm của sàn nhà và đường thẳng đi qua O song song với a.
Tương tự, ta xác định được các điểm A', B', C', D'.

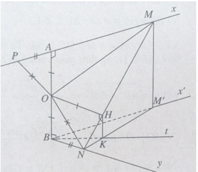
Theo giả thiết ta có M và N là hai điểm di động lần lượt trên hai tia Ax và By sao cho AM + BN = MN.
a) Kéo dài MA một đoạn AP = BN, ta có MP = MN và OP = ON.
Do đó ΔOMP = ΔOMN (c.c.c)
⇒ OA = OH nên OH = a.
Ta suy ra HM = AM và HN = BN.
b) Gọi M’ là hình chiếu vuông góc của điểm M trên mặt phẳng (Bx’, By) ta có:
HK // MM’ với K ∈ NM’.
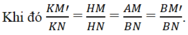
Do đó đối với tam giác BNM’ đường thẳng BK là phân giác của góc (x'By) .
c) Gọi (β) là mặt phẳng (AB, BK). Vì HK // AB nên HK nằm trong mặt phẳng (β) và do đó H thuộc mặt phẳng (β). Trong mặt phẳng (β) ta có OH = a. Vậy điểm H luôn luôn nằm trên đường tròn cố định, đường kính AB và nằm trong mặt phẳng cố định (β) = (AB, BK)

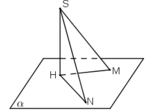
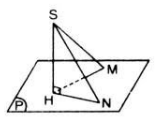
Giả sử ta có hai đường xiên SM, SN và các hình chiếu HM, HN của chúng trên mp (α).
Vì SH ⊥ mp(α)
⇒ SH ⊥ HM và SH ⊥ HN
⇒ ΔSHN và ΔSHM vuông tại H.
Áp dụng định lí Py-ta- go vào hai tam giác vuông này ta có:
⇒ S M 2 = S H 2 + H M 2 ; v à S N 2 = S H 2 + H N 2 . a ) S M = S N ⇔ S M 2 = S N 2 ⇔ H M 2 = H N 2 ⇔ H M = H N . b ) S M > S N ⇔ S M 2 > S N 2 ⇔ H M 2 > H N 2 ⇔ H M > H N .

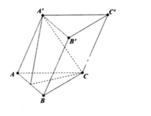
Gọi O là trung điểm của AC
Hình bình hành ACC'A' có: OO' // AA'
Vì O thuộc (ABCD)
Do đó: O là ảnh của O'.

a: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
CD vuông góc SA
CD vuông góc AD
=>CD vuông góc (SAD)
b: \(SD=\sqrt{a^2+a^2}=a\sqrt{2}\)

a) Giả sử ta có hai đường xiên SA, SB và các hình chiếu HA, HB của chúng trên mp(α)
Giả sử HA = HB
Vì SH ⊥ mp(α) nên SH ⊥ HA và SH ⊥ SB và các tam giác SHA, SHB là các tam giác vuông. Hai tam giác vuông SHA, SHB có canh SH chung và HA = HB nên :
ΔSHA = ΔSHB SA = SB
Ngược lại nếu SA = SB thì ΔSHA = ΔSHB ⇒ HA = HB
Kết quả, ta có HA = HB SA= SB (đpcm)
b) Giả sử có hai đường xiên SA, SC và các hình chiếu HA, HC của chúng trên mp(α) với giả thiết HC > HA.
Trên đoạn HC, lấy điểm B' sao cho HA' = HA ⇒ HC > HA'. Như vậy, theo kết quả câu a) ta có SA' = SA. Ta có trong các tam giác vuông SHB', SHC thì :
SC2= SH2 + HC2
SA2 = SH2 + HA2
Vì HC > HA' nên SC2 > SA2 ⇒ SC > SA
Suy ra SC > SA
Như vậy HC > HA ⇒ SC > SA
Lí luận tương tự, ta có : SC > SA ⇒ HC > HA
Kết quả : HC > HA ⇔ SC > SA
a) Gọi SN là một đường xiên khác. Xét hai tam giác vuông SHM và SHN có SH chung. Nếu SM = SN => tam giác SHM = tam giác SHN => HM = HN, ngược lại nếu HM = HN thì tam giác SHM = tam giác SHNSM => SM = SN.
b) Xét tam giác vuông SHM và SHN có SH chung. Nếu SN > SM thì \(HN^2-SN^2-SH^2\) => \(SM^2-SH^2=HM^2\) => HN > HM. Chứng minh tương tự cho chiều ngược lại.

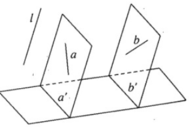
Giả sử a và b là hai đường thẳng chéo nhau có hình chiếu là a' và b'. Nếu mặt phẳng (a, a') và mặt phẳng (b, b') song song với nhau thì a′ // b′. Vậy hình chiếu song song của hai đường thẳng chéo nhau có thể song song.
Nếu a và b là hai đường thẳng cắt nhau tại O và hình chiếu của O là O' thì O′ ∈ a′ và O′ ∈ b′ tức là a' và b' có điểm chung. Vậy hình chiếu song song của hai đường thẳng cắt nhau không thể song song được.



a) Hình chiếu O’ của điểm O nằm trên đoạn A’C’.
b) Hình chiếu song song của AB và CD song song với AB và CD.
c) Hình chiếu O’ của điểm O là trung điểm của đoạn A’C’.