Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Theo tính chất của cấp số cộng ta có:
1+ sin x + 1 + sin 3x = 2sin2x
⇔ 2 + 4sin x – 4sin3 x = 2sin2x
⇔ 2sin3x + sin2x – 2sin x – 1 = 0
⇔ (2sin x + 1)(sin2x – 1) = 0
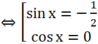
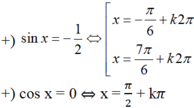
Với nghiệm 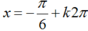 và x ∈ [0;2π], ta tìm được
và x ∈ [0;2π], ta tìm được 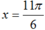 .
.
Với nghiệm 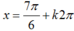 và x ∈ [0;2π], ta tìm được
và x ∈ [0;2π], ta tìm được 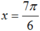 .
.
Với nghiệm ![]() và x ∈ [0;2π] ta tìm được nghiệm
và x ∈ [0;2π] ta tìm được nghiệm 
Do đó 

Chọn A
Theo giả thiết ta có :
y = x q ; z = x q 2 x + 3 z = 2 2 y ⇒ x + 3 x q 2 = 4 x q ⇒ x 3 q 2 − 4 q + 1 = 0 ⇔ x = 0 3 q 2 − 4 q + 1 = 0 .
Nếu x = 0 ⇒ y = z = 0 ⇒ công sai của cấp số cộng: x ; 2y ; 3z bằng 0 (vô lí).
nếu
3 q 2 − 4 q + 1 = 0 ⇔ q = 1 q = 1 3 ⇔ q = 1 3 q = 1 .

Chọn C
3 số : ln 2 ; ln ( 2 x - 1 ) ; ln ( 2 x + 3 ) lập thành cấp số cộng
⇒ 2 x = 2 + 11 ⇒ x ≈ 25

Ba số \(2x-1;x;2x+1\) là một cấp số nhân khi:
\(\left(2x-1\right)\left(2x+1\right)=x^2\)
\(\Leftrightarrow\left(2x\right)^2-1^2=x^2\)
\(\Leftrightarrow4x^2-1=x^2\)
\(\Leftrightarrow4x^2-x^2=1\)
\(\Leftrightarrow3x^2=1\)
\(\Leftrightarrow x^2=\dfrac{1}{3}\)
\(\Leftrightarrow x=\pm\sqrt{\dfrac{1}{3}}\)
\(\Leftrightarrow x=\pm\dfrac{\sqrt{3}}{3}\)
Vậy \(2x-1;x;2x+1\) là một cấp số nhân khi \(x=\pm\dfrac{\sqrt{3}}{3}\)

1: Để đây là cấp số cộng thì
\(\left\{{}\begin{matrix}x=\dfrac{2+8}{2}=\dfrac{10}{2}=5\\8=\dfrac{y+x}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=5\\y+5=16\end{matrix}\right.\)
=>x=5 và y=11
2: Để bốn số này là cấp số cộng thì
\(\left\{{}\begin{matrix}a+b+1=2\cdot5=10\\b+1=\dfrac{5+13}{2}=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=8\\a=1\end{matrix}\right.\)

Chọn A.
+ Điều kiện cần: Giả sử phương trình đã cho có ba nghiệm phân biệt x1; x2; x3 lập thành một cấp số nhân.
Theo định lý Vi-ét, ta có x1.x2.x3 = 64
Theo tính chất của cấp số nhân, ta có x1x3 = x22. Suy ra ta có x23 = 64 ⇔ x2 = 4
Thay x = 4 vào phương trình đã cho ta được: 43 – 7m.42 + 2(m2 + 6m).4 – 64 = 0
⇔ m2 – 8m = 0
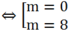
+ Điều kiện đủ: Với m = 0 thay vào phương trình đã cho ta được: x3 – 64 = 0 hay x = 4
(nghiệm kép-loại)
Với m = 8 thay vào phương trình đã cho nên ta có phương trình x3 – 56x2 + 224x – 64 = 0
Giải phương trình này, ta được 3 nghiệm phân biệt lập thành cấp số nhân.
Vậy m = 8 là giá trị cần tìm.

Theo giả thiết ta có : \(\begin{cases}\left(5x-y\right)+\left(x+2y\right)=2\left(2x+3y\right)\\\left(y+1\right)^2\left(x-1\right)^2=\left(xy+1\right)^2\end{cases}\)
\(\Leftrightarrow\begin{cases}2x=5y\\x+y=2\end{cases}\) hoặc \(\Leftrightarrow\begin{cases}2x=5y\\xy+x+y=0\end{cases}\)
\(\Leftrightarrow\begin{cases}2x=5y\\x+y=2\end{cases}\) hoặc \(\Leftrightarrow\begin{cases}2x=5y\\y\left(5y\right)+5y+2y=0\end{cases}\)
\(\Leftrightarrow\begin{cases}x=\frac{10}{3}\\y=\frac{4}{3}\end{cases}\) hoặc \(\begin{cases}x=0,y=0\\x=-\frac{3}{4},y=-\frac{3}{10}\end{cases}\)
Để 3 số hạng đó lập thành cấp số cộng, ta có :
\(\left(5^{1+x}+5^{1-x}\right)+\left(25^x+25^{-x}\right)=2\left(\frac{a}{2}\right)\)
\(\Leftrightarrow a=5\left(5^x+\frac{1}{5^x}\right)+\left(5^{2x}+\frac{1}{5^{2x}}\right)\)
Theo bất đẳng thức côsi, ta có : \(5^x+\frac{1}{5^x}\ge2\sqrt{1}=2,5^{2x}+\frac{1}{5^{2x}}\ge2\)
\(\Rightarrow a\ge5.2+2=12\)
Vậy với : \(a\ge12\), thì 3 số đó lập thành cấp số cộng.