Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
y' = - .
a) Ta có: \(y'\left(x_0\right)=k\Leftrightarrow\) y' = -4. \(\Rightarrow\)k= -4. Vậy phương trình tiếp tuyến của hypebol tại điểm (
; 2) là y - 2 = -4(x -
) hay y = -4x + 4.
b)Ta có:\(y'\left(x_0\right)=k\Leftrightarrow\) y' (-1) = -1.\(\Rightarrow\) k= -1. Ngoài ra, ta có y(-1) = -1. Vậy phương trình tiếp tuyến tại điểm có tọa độ là -1 là
y - (-1) = -[x - (-1)] \(\Leftrightarrow\) y = -x - 2.
c) Gọi x0 là hoành độ tiếp điểm. Ta có
y' (x0) = - <=> -
= -
<=> x02 = 4 <=> x0 = ±2.
Với x0 = 2 ta có y(2) = , phương trình tiếp tuyến là
y - = -
(x - 2) \(\Leftrightarrow\) y =
x + 1.
Với x0 = -2 ta có y (-2) = - , phương trình tiếp tuyến là
y - = -
[x - (-2)] \(\Leftrightarrow\) y = -
x -1
Với mọi x0 ∈ R ta có:
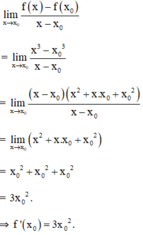
a) Tiếp tuyến của y = x3 tại điểm (-1; -1) là:
y = f’(-1)(x + 1) + y(1)
= 3.(-1)2(x + 1) – 1
= 3.(x + 1) – 1
= 3x + 2.
b) x0 = 2
⇒ y0 = f(2) = 23 = 8;
⇒ f’(x0) = f’(2) = 3.22 = 12.
Vậy phương trình tiếp tuyến của y = x3 tại điểm có hoành độ bằng 2 là :
y = 12(x – 2) + 8 = 12x – 16.
c) k = 3
⇔ f’(x0) = 3
⇔ 3x02 = 3
⇔ x02 = 1
⇔ x0 = ±1.
+ Với x0 = 1 ⇒ y0 = 13 = 1
⇒ Phương trình tiếp tuyến : y = 3.(x – 1) + 1 = 3x – 2.
+ Với x0 = -1 ⇒ y0 = (-1)3 = -1
⇒ Phương trình tiếp tuyến : y = 3.(x + 1) – 1 = 3x + 2.
Vậy có hai phương trình tiếp tuyến của đường cong y = x3 có hệ số góc bằng 3 là y = 3x – 2 và y = 3x + 2.
\(f'\left(x\right)=3x^2-6x+1\Rightarrow f'\left(1\right)=-2\)
Phương trình tiếp tuyến tại điểm có hoành độ bằng 1 là:
\(\Delta:y=f'\left(1\right)\left(x-1\right)+f\left(1\right)\Rightarrow y=\left(-2\right)\left(x-1\right)-2\)
Ta có y'=3x^2 - 6x +1
gọi M(x0;y0) là tiếp điểm
Ta có x0 =1 do đó yo =1^3 -3.1^2+1-1=-2
y'(1)=3.1^2-6.1+1=-2
Vậy phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 1 là y=y'(1)(x-1)+(-2)=>y=-2x
a) Ta có:
y′=f′(x)=−2(x−1)2⇒f′(2)=−2(2−1)2=−2y′=f′(x)=−2(x−1)2⇒f′(2)=−2(2−1)2=−2
Suy ra phương trình tiếp tuyến cần tìm là:
y – 3 = -2(x – 2) ⇔ y = -2x + 7
b) Ta có: y’ = f’(x) = 3x2 + 8x ⇒ f’(-1) = 3 – 8 = -5
Mặt khác: x0 = -1 ⇒ y0 = -1 + 4 – 1 = 2
Vậy phương trình tiếp tuyến cần tìm là:
y – 2 = -5 (x + 1) ⇔ y = -5x – 3
c) Ta có:
y0 = 1 ⇒ 1 = x2 – 4x + 4 ⇒ x02 – 4x0 + 3 = 0 ⇒ x0 = 1 hoặc x0 = 3
f’(x) = 2x – 4 ⇒ f’(1) = -2 và f’(3) = 2
Vậy có hai tiếp tuyến cần tìm có phương trình là:
y – 1 = -2 (x – 1) ⇔ y = -2x + 3
y – 1 = 2 (x – 3) ⇔ y = 2x – 5
Ta có: Với mọi x0 ≠ 0:
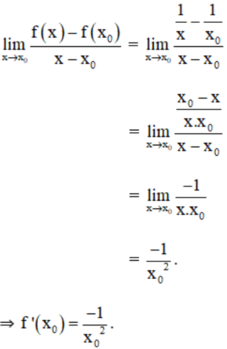
b) Tại x0 = -1
⇒ y0 = -1
⇒ f’(x0) = -1.
Vậy phương trình tiếp tuyến của đường cong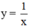 
tại điểm có hoành độ -1 là:
y = -1(x + 1) – 1 = -x – 2.
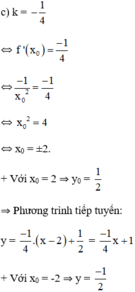
⇒ Phương trình tiếp tuyến:
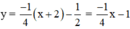
Vậy có hai phương trình tiếp tuyến của hypebol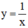 
có hệ số góc 
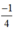bằng
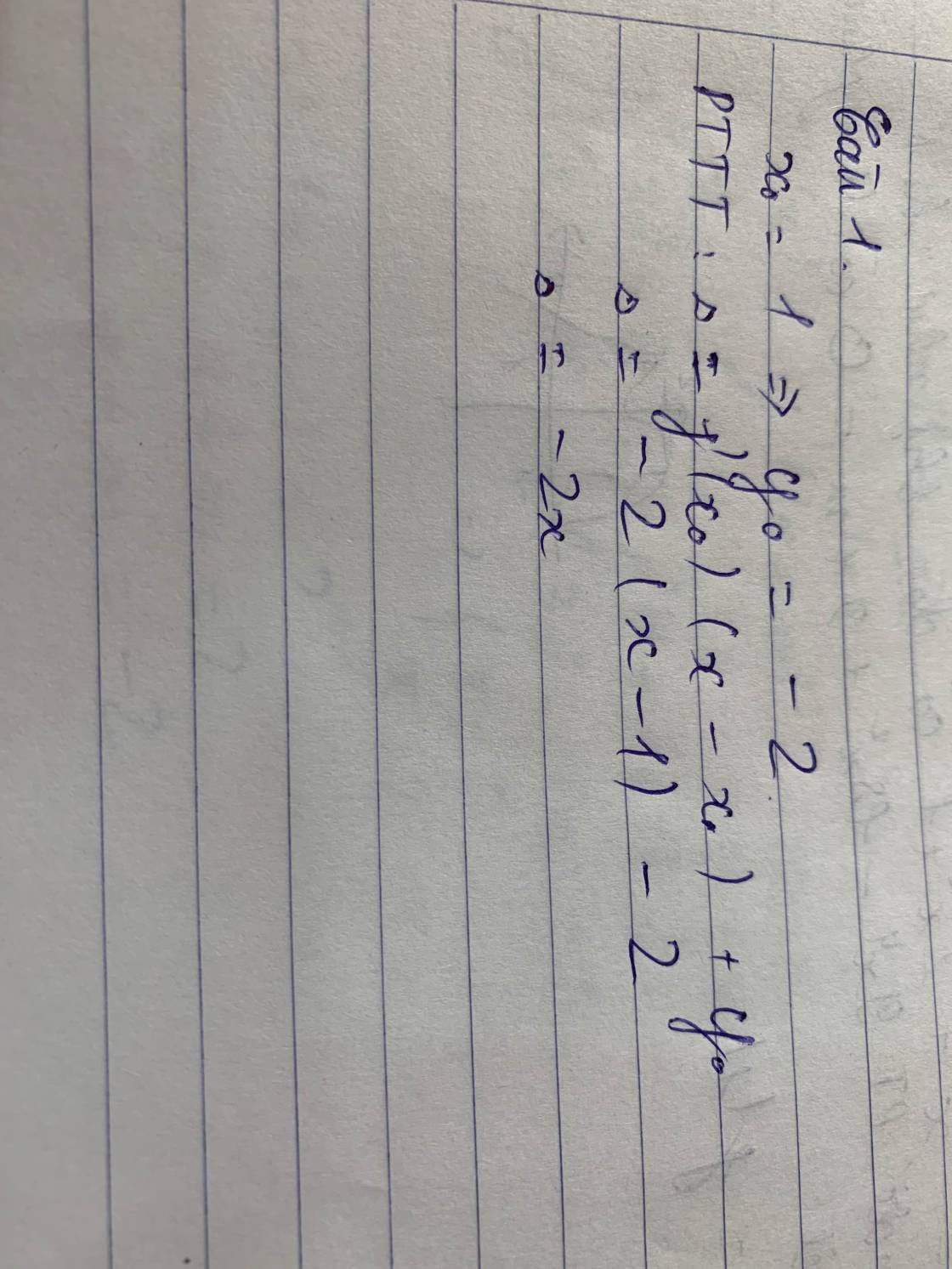
y' = 3x2.
a)Ta có: \(y'\left(x_0\right)=k\Leftrightarrow\) y' (-1) = 3. \(\Rightarrow\) k=3. Vậy phương trình tiếp tuyến tại điểm (-1;-1) là : y - (-1) = 3[x - (-1)] \(\Leftrightarrow\) y = 3x+2.
b) Ta có:\(y'\left(x_0\right)=k\Leftrightarrow\)y' (2) = 12. \(\Rightarrow\) k=12. Ngoài ra ta có y(2) = 8. Vậy phương trình tiếp tuyến tại điểm có hoành độ bằng 2 là:
y - 8 = 12(x - 2) \(\Leftrightarrow\) y = 12x -16.
c) Gọi x0 là hoành độ tiếp điểm. Ta có:
y' (x0) = 3 <=> 3x02 = 3 <=> x02= 1 <=> x0 = ±1.
Với x0 = 1 ta có y(1) = 1, phương trình tiếp tuyến là
y - 1 = 3(x - 1) \(\Leftrightarrow\) y = 3x - 2.
Với x0 = -1 ta có y(-1) = -1, phương trình tiếp tuyến là
y - (-1) = 3[x - (-1)] \(\Leftrightarrow\) y = 3x + 2