
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vẽ lại các tứ giác ở hình 9, hình 10 sgk vào vở
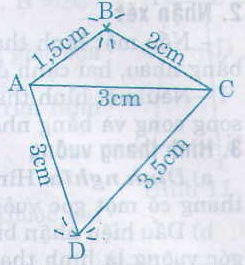
* Cách vẽ hình 9: Vẽ tam giác ABC trước rồi vẽ tam giác ACD (hoặc ngược lại).
- Vẽ đoạn thẳng AC = 3cm.
- Trên cùng một nửa mặt phẳng bờ AC, vẽ cung tròn tâm A bán kính 1,5cm với cung tròn tâm C bán kính 2cm.
- Hai cung tròn trên cắt nhau tại B.
- Vẽ các đoạn thẳng AB, AC ta được tam giác ABC.
Tương tự ta sẽ được tam giác ACD.
Tứ giác ABCD là tứ giác cần vẽ.
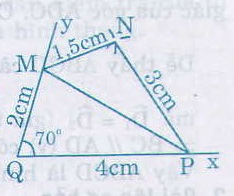
* Cách vẽ hình 10: Vẽ tam giác MQP trước rồi vẽ tam giác MNP.
Vẽ tam giác MQP biết hai cạnh và góc xen giữa.
- Vẽ góc ˆxOy=700xOy^=700
- Trên tia Qx lấy điểm M sao cho QM = 2cm.
- Trên tia Qy lấy điểm P sao cho QP= 4cm.
- Vẽ đoạn thẳng MP, ta được tam giác MQP.
Vẽ tam giác MNP biết ba cạnh, với cạnh MP đã vẽ. Tương tự cách vẽ hình 9, điểm N là giao điểm của hai cung tròn tâm M, P bán kính lần lướt là 1,5cm; 3cm.
Tứ giác MNPQ là tứ giác cần vẽ.
Bài giải:
Vẽ lại các tứ giác ở hình 9, hình 10 sgk vào vở
* Cách vẽ hình 9: Vẽ tam giác ABC trước rồi vẽ tam giác ACD (hoặc ngược lại).
- Vẽ đoạn thẳng AC = 3cm.
- Trên cùng một nửa mặt phẳng bờ AC, vẽ cung tròn tâm A bán kính 1,5cm với cung tròn tâm C bán kính 2cm.
- Hai cung tròn trên cắt nhau tại B.
- Vẽ các đoạn thẳng AB, AC ta được tam giác ABC.
Tương tự ta sẽ được tam giác ACD.
Tứ giác ABCD là tứ giác cần vẽ.

* Cách vẽ hình 10: Vẽ tam giác MQP trước rồi vẽ tam giác MNP.
Vẽ tam giác MQP biết hai cạnh và góc xen giữa.
- Vẽ góc ˆxOy=700xOy^=700
- Trên tia Qx lấy điểm M sao cho QM = 2cm.
- Trên tia Qy lấy điểm P sao cho QP= 4cm.
- Vẽ đoạn thẳng MP, ta được tam giác MQP.
Vẽ tam giác MNP biết ba cạnh, với cạnh MP đã vẽ. Tương tự cách vẽ hình 9, điểm N là giao điểm của hai cung tròn tâm M, P bán kính lần lướt là 1,5cm; 3cm.
Tứ giác MNPQ là tứ giác cần vẽ.


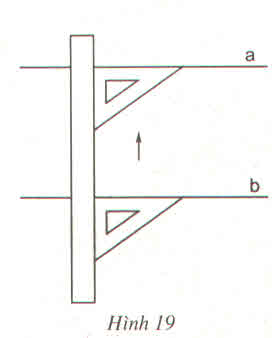
Các bước tiến hành:
- Xét xem cần phải kiểm tra hai cạnh nào thuộc hai đường thẳng song song với nhau.
- Đặt mép cạnh góc vuông của êke trùng với một trong hai cạnh cần kiểm tra.
- Đặt mép thước trùng với mép cạnh góc vuông còn lại của êke.
- Giữ nguyên vị trí thước, dời êke để xét xem cạnh góc vuông của êke có trùng với cạnh còn lại mà ta cần kiểm tra của tứ giác. Nếu chúng trùng nhau thì tứ giác đó là hình thang.
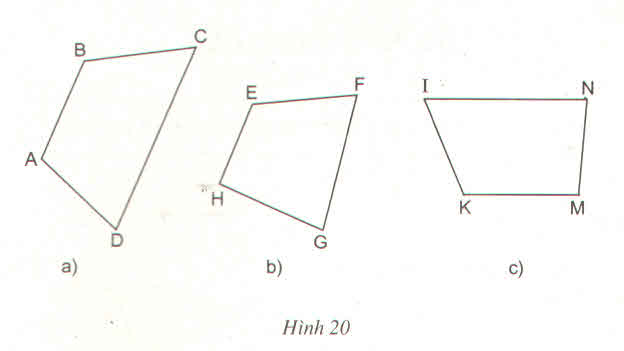
Các tứ giác ABCD, IKMN là hình thang.
Tứ giác EFGH không là hình thang.
Bài giải:
Các bước tiến hành:
- Xét xem cần phải kiểm tra hai cạnh nào thuộc hai đường thẳng song song với nhau.
- Đặt mép cạnh góc vuông của êke trùng với một trong hai cạnh cần kiểm tra.
- Đặt mép thước trùng với mép cạnh góc vuông còn lại của êke.
- Giữ nguyên vị trí thước, dời êke để xét xem cạnh góc vuông của êke có trùng với cạnh còn lại mà ta cần kiểm tra của tứ giác. Nếu chúng trùng nhau thì tứ giác đó là hình thang.
Các tứ giác ABCD, IKMN là hình thang.
Tứ giác EFGH không là hình thang.

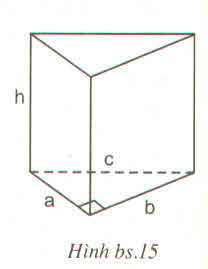
| a | 9 | 35 | 20 | 63 | 28 |
| b | 40 | 12 | 21 | 16 | 45 |
| c | 41 | 37 | 29 | 65 | 53 |
| h | 8 | 18 | 17 | 24 | 13 |
| Diện tích 1 đáy | 180 | 210 | 210 | 504 | 630 |
| Diện tích xung quanh | 720 | 1512 | 1190 | 3456 | 1638 |
| Diện tích toàn phần | 1080 | 1932 | 1610 | 4464 | 2898 |
| Thể tích | 1440 | 3780 | 3570 | 12096 | 8190 |

Tứ giác ABCD là hình bình hành vì hai cạnh đối AD, BC song song và bằng nhau.
Tứ giác IKMN là hình bình hành vì KM // IN, IK // MN (hoặc vì \(\widehat{I}=\widehat{M},\widehat{K}=\widehat{N}\) )
Tứ giác ABCD là hình bình hành
Tứ giác IKMN là hình bình hành

Cả ba tứ giác là hình bình hành.
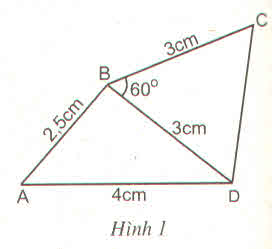
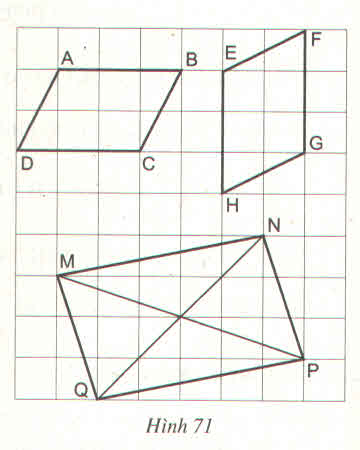
- Tứ giác ABCD là hình bình hành vì có
AB // CD và AB = CD =3 (dấu hiệu nhận biết 3)
- Tứ giác EFGH là hình bình hành vì có
EH // FG và EH = FH = 3 (dấu hiệu nhận biết 3)
- Tứ giác MNPQ là hình bình hành vì có MN = QP và MQ = NP (dấu hiệu nhận biết 2)

Bài giải:
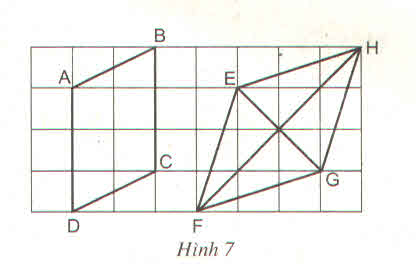
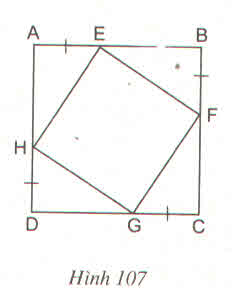
Các tam giác vuông AEH, BFC, CGF, DHG có:
AE = BF = CG = DH (gt)
Suy ra AH = BE = CF = DG
Nên ∆AEH = ∆BFE = ∆CGF = ∆DHG (c.g.c)
Do đó HE = EF = FG = GH (1)
và ˆEHAEHA^ = ˆFEBFEB^
Ta có ˆHEFHEF^ = 1800 - (ˆHEAHEA^ + ˆFEBFEB^) = 1800 - (ˆHEAHEA^ + ˆEHAEHA^)
= 1800 - 900 = 900 (2)
Từ (1) và (2) ta được EFGH là hình vuông
Các tam giác vuông AEH, BFC, CGF, DHG có:
AE = BF = CG = DH (gt)
Suy ra AH = BE = CF = DG
Nên ∆AEH = ∆BFE = ∆CGF = ∆DHG (c.g.c)
Do đó HE = EF = FG = GH (1)
và ˆEHAEHA^ = ˆFEBFEB^
Ta có ˆHEFHEF^ = 1800 - (ˆHEAHEA^ + ˆFEBFEB^) = 1800 - (ˆHEAHEA^ + ˆEHAEHA^)
= 1800 - 900 = 900 (2)
Từ (1) và (2) ta được EFGH là hình vuông.








Chép ở lời giải - chỉ dẫn - đáp số trong Bài tập Toán