Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo tính chất trung tuyến, suy ra:
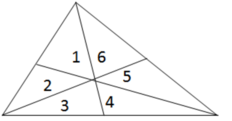
S1 = S2 (có đáy bằng nhau và cùng chiều cao) (1)
S3 = S4 (có đáy bằng nhau và cùng chiều cao) (2)
S5 = S6 (có đáy bằng nhau và cùng chiều cao) (3)
Ta có: S1 + S2 + S3 = S4 + S5 + S6 (= 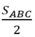 )
)
⇔ 2S1 + S3= S4 + 2S6 ( vì S1= S2; S5 = S6)
⇔ 2S1 = 2S6( vì S3 = S4)
⇔ S1 = S6.
Và S1+ S2+ S6 = S3 + S4 +S5 = 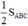 (5)
(5)
Kết hợp (5) với (1), (2), (3) suy ra S2 = S3 (5’)
Và S1 + S5 + S6 = S2+ S3 + S4 = 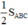 (6)
(6)
Kết hợp (6) với (1), (2), (3) suy ra S4 = S5 (6’)
Từ (4’), (5’), (6’) và kết hợp (1) (2) (3) ta có: S1= S2 = S3 = S4 = S5 = S6

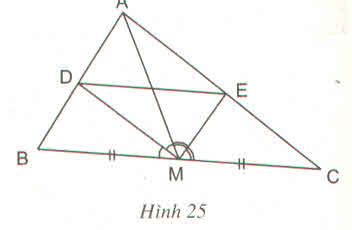
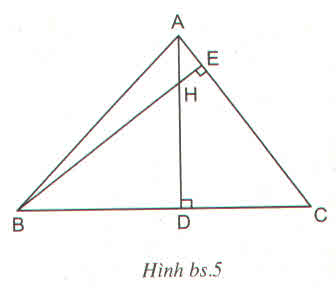
Ta có MD là đường phân giác của tam giác ABM
=> ADBDADBD = AMBMAMBM (1)
ME là đường phân giác của tam giác ACM
=> AECEAECE = AMMCAMMC (2)
Mà MB = MC( AM là đường trung tuyến)
=> AMBMAMBM = AMMCAMMC (3)
từ 1,2,3 => ADBDADBD = AECEAECE => DE // BC( Định lí Talet đảo)

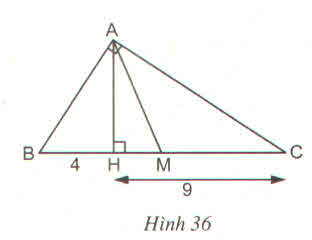
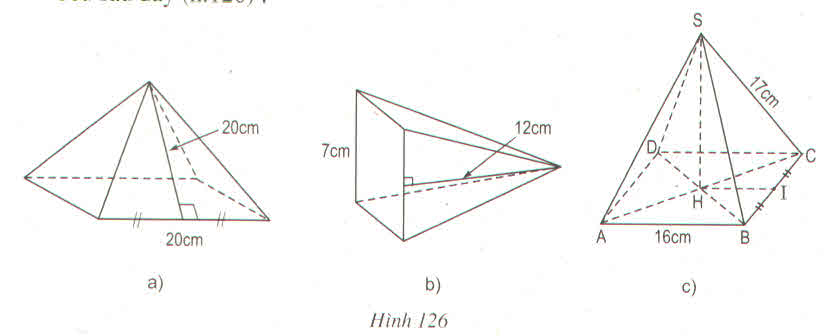
Hình a : Sxq = p.d = \(\dfrac{1}{2}\).20.4.20 = 800(cm2)
Diện tích đáy: Sđ = 202 = 400(cm2)
Diện tích toàn phần của lăng trụ hai là:
Stp = Sxq + Sđ = 800 + 400 = 1200(cm2)
Hình b: Sxq = p.d = \(\dfrac{1}{2}\).7.4.12 = 168(cm2)
Sđ = 72 = 49(cm2)
Stp = Sxq + Sđ = 168 + 49 = 217(cm2)
Hình c: Chiều cao của mặt bên của hình chóp:
\(h=\sqrt{17^2-8^2}=\sqrt{225}=15\left(cm\right)\)
Sxq = p.d = \(\dfrac{1}{2}\).16.4.15 = 480(cm2)
Sđ = 162 = 256(cm2)
Stp = Sxq + Sđ = 480 + 256 = 736(cm2)

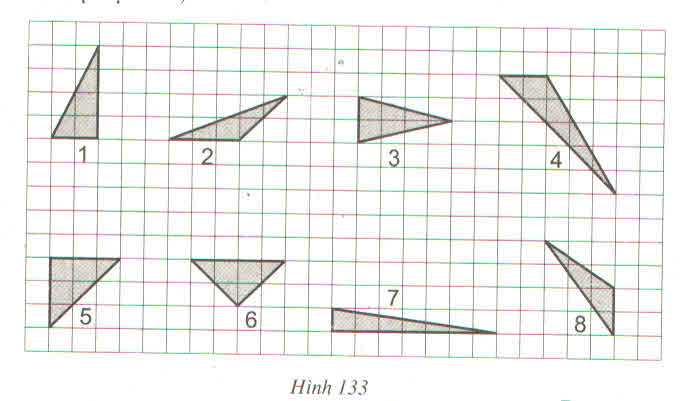
a) Các tam giác số 1, 3, 6 có cùng diện tích là 4 ô vuông.
Các tam giác số 2, 8 có cùng diện tích là 3 ô vuông.
Các tam giác số 4, 5, 7 không có cùng diện tích với các tam giác nào khác(diện tích tam giác số 4 là 5 ô vuông, tam giác số là 4,5 ô vuông, tam giác số 7 là 3,5 ô vuông).
b) Hai tam giác có diện tích bằng nhau thì chưa chắc hai tam giác đó đã bằng nhau.
a) Các tam giác số 1, 3, 6 có cùng diện tích là 4 ô vuông.
Các tam giác số 2, 8 có cùng diện tích là 3 ô vuông.
Các tam giác số 4, 5, 7 không có cùng diện tích với các tam giác nào khác(diện tích tam giác số 4 là 5 ô vuông, tam giác số là 4,5 ô vuông, tam giác số 7 là 3,5 ô vuông).
b) Hai tam giác có diện tích bằng nhau thì chưa chắc hai tam giác đó đã bằng nhau.


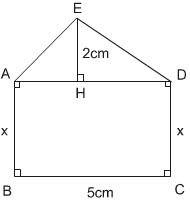
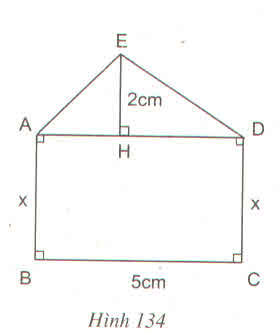
Ta có AD = BC = 5cm
Diện tích ∆ADE: SADE =  2.5 = 5(cm)
2.5 = 5(cm)
Diện tích hình chữ nhật ABCD: SABCD = 5x
Theo đề bài ta có
SABCD= 3SADE nên 5x = 3.5
Vậy x = 3cm