Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

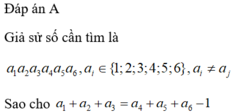
![]()
![]()
![]()
![]()
Vậy số cách để lập số có 6 chữ số khác nhau sao cho tổng ba số đầu nhỏ hơn tổng ba số cuối một đơn vị là: ![]()

Đáp án B
Số cần lập là a b c d e f , ta có a + b + c – 1 = d + e + f <=> 20 = 2(d + e + f) <=> d + e + f = 10
Với mỗi f ∈ { 1 ; 3 ; 5 } => d, e có 4 cách chọn, suy ra a b c d e f có 4.3! = 24 cách chọn
Suy ra có 3.24 = 72 số có thể lập thỏa mãn đề bài.

Gọi ![]() là số cần lập a1 + a2 + a3 = 10
là số cần lập a1 + a2 + a3 = 10
Theo bài ra ta có: ![]() (1)
(1)
Mà ![]() và đôi một khác nhau nên
và đôi một khác nhau nên
a1,a2,a3,a4,a5,a6 = 1 + 2 + 3 + 4 + 5 + 6 =21
(2)
Từ (1), (2) suy ra: a1 + a2 + a3 = 10
Phương trình này có các bộ nghiệm là: ( a1 , a2 , a3 ) = (1,3,6); (1,4,5); (2,3,5)
Với mỗi bộ ta có 3!.3!=36 số.
Vậy có cả 3.36=108 số cần lập.
Chọn C.

Chọn đáp án C
Cách 1: Gọi x = a 1 a 2 . . . a 6 ¯ , a i ∈ 1 , 2 , 3 , 4 , 5 , 6 là số cần lập
Theo bài ra ta có:
![]()
Mà a 1 , a 2 , a 3 , a 4 , a 5 , a 6 ∈ 1 , 2 , 3 , 4 , 5 , 6 và đôi một khác nhau nên
![]()
Từ (1), (2) suy ra: a 1 + a 2 + a 3 = 10
Phương trình này có các bộ nghiệm là:
![]()
Với mỗi bộ ta có 36 số.
Vậy có cả thảy 3.36=108 số cần lập.
Cách 2: Gọi x = a b c d e f là số cần lập
Ta có:
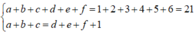
⇒ a + b + c = 11 .
Do a , b , c ∈ 1 , 2 , 3 , 4 , 5 , 6
Suy ra ta có các cặp sau:
![]()
Với mỗi bộ như vậy ta có 3! cách chọn a, b, c và 3! cách chọn d ,e ,f
Do đó: 3!.3!.3!= 108 số thỏa yêu cầu bài toán

Ta có 1+2+3+4+5+6+ =21 Vậy tổng của 3 chữ số đầu là 10
Dễ thấy 1+3+6 = 1+4+5 = 2+3+5
Vậy có 3 cách chọn 3 nhóm 3 chữ số đầu (1,3,6 hoặc 1,4,5 hoặc 2,3,5)
Với 1 cách chọn nhóm 3 chữ số thì có 3! cách để lập ra số \(\overline{a_1a_2a_3}\)
Với 3 số còn lại thì có 3! cách để lập ra số \(\overline{a_4a_5a_6}\)
(ở đây \(\overline{a_1a_2a_3a_4a_5a_6}\) là số thỏa mãn yêu cầu đề ra)
Theo quy tắc nhân ta có 3.6.6 = 108
Vậy có 108 số cần tìm
Em thấy như này còn thiều trường hợp hay sao ý ạ tại ba số nhỏ hơn đâu nhất thiết phải bằng 10 ạ 123 vs 345 vẫn tỏa mãn đấy chứ ạ.Có thể cho em là mình sai ở đâu hay kế quả thế nào được không ạ??

Gọi số đó là \(\overline{abcdef}\Rightarrow a+b+c+d+e+f=1+2+3+4+5+6=21\)
Mặt khác \(a+b+c=d+e+f-1\)
\(\Rightarrow\left\{{}\begin{matrix}a+b+c=10\\d+e+f=11\end{matrix}\right.\)
\(\Rightarrow\left(a;b;c\right)=\left(1;3;6\right);\left(1;4;5\right);\left(2;3;5\right)\)
Số số thỏa mãn: \(3.\left(3!.3!\right)=108\)
Xác suất: \(P=\dfrac{108}{6!}=\dfrac{3}{20}\)

Chọn D
Từ các chữ số 1; 2; 3; 4; 5; 6 ta lập các số tự nhiên có 6 chữ số khác nhau, lập được 6! = 720 số. Vậy số phần tử của không gian mẫu là n ( Ω ) = 720 số
Gọi a b c d e f ¯ là số tự nhiên có 6 chữ số khác nhau thuộc biến cố A.
Ta có: 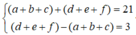
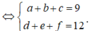
Từ sáu chữ số 1; 2; 3; 4; 5; 6 ta phân chia thành bộ ba số có tổng là 9 và bộ ba số có tổng là 12, có 3 cách phân chia, đó là (1;2;6) và (3;4;5), (1;3;5) và (2;4;6), (2;3;4) và (1;5;6). Trong mỗi cách phân chia này, ta lập được 3!.3! = 36 số. Do đó n(A) = 3.36 = 108.
Vậy xác suất của biến cố A là:
![]()

Các bộ 3 số thỏa mãn: (1;2;7);(1;3;6);(1;4;5);(2;3;5) tổng cộng 4 bộ số
Với mỗi bộ số ta có \(3!\) cách hoán vị
Do đó có: \(3!.4=24\) số

Tổng 3 chữ số đầu và 3 chữ số cuối là 2+3+4+5+6+7=27, hiệu của chúng là 3
\(\Rightarrow\) Tổng 3 chữ số đầu là 12
\(\Rightarrow\) 3 chữ số đầu là (2;3;7); (2;4;6);(3;4;5) có 3 trường hợp (với mỗi bộ 3 chữ số đầu sẽ có đúng 1 bộ 3 chữ số cuối tương ứng)
\(\Rightarrow\) Có \(3.3!.3!=108\) số thỏa mãn