Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
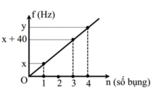
a) Trên dây sợi dây có hai đầu cố định, xuất hiện 6 bụng sóng nên chọn n = 6.
Áp dụng công thức: \(l=n\dfrac{v}{2f}\Rightarrow0,75=6\cdot\dfrac{v}{2\cdot120}\Rightarrow v=30m/s\)
b) Tăng tốc độ truyền sóng gấp hai lần: \(v'=2v=2\cdot30=60m/s\)
\(\Rightarrow l=n\dfrac{v'}{2f}\Rightarrow f=\dfrac{nv'}{2l}=\dfrac{n\cdot60}{2\cdot0,75}=40n\)
Với n = 1 thì f = 40 Hz
Với n = 2 thì f = 80 Hz
Với n = 3 thì f = 120 Hz
Với n = 4 thì f = 160 Hz
…
Vậy với các giá trị tần số thoả mãn f = 40 n (với n = 1; 2; 3;…) thì trên dây có sóng dừng và tốc độ truyền sóng là 60 m/s

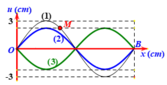
Điều kiện để xuất hiện sóng dừng trên dây có hai đầu cố định là L = \(n\frac{\lambda }{2}\)
Từ hình vẽ ta thấy trên dây xuất hiện 3 bụng sóng ⇒ n = 3
⇒ λ=\(\frac{{2L}}{n}\) = \(\frac{{2.1,2}}{3}\)= 0,8 (m)
Tốc độ sóng truyền trên dây là: v = λf = 0,8.13,3 = 10,64 (m/s)



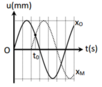
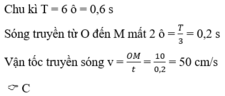
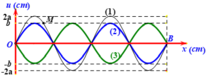

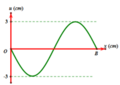

a) Ngoài đầu A, trên dây xuất hiện thêm một nút nên ta có
\(l = 3\frac{\lambda }{4} \Rightarrow \lambda = 160cm\)
Tốc độ truyền sóng là: v=f.λ=12,5.160=2000cm/s
b) Để có thêm một nút sóng thì
\(l = 5\frac{\lambda }{4} \Rightarrow f = \frac{\lambda }{4}\frac{v}{{\frac{4}{5}l}} = \frac{{2000}}{{\frac{4}{5}.120}} = 20,833Hz\)