Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình BC: 3x + 4y - 4 =0
=> d(A; BC) = \(\frac{\left|3.1+4.4-4\right|}{\sqrt{3^2+4^2}}\) = 3
=> Đáp án C

a) Khoảng cách từ điểm A đến đường thẳng \(\Delta \) là: \(d\left( {A,\Delta } \right) = \frac{{\left| {0 - 2 - 4} \right|}}{{\sqrt {{1^2} + {1^2}} }} = 3\sqrt 2 \).
b) Ta có: \(\overrightarrow {{n_a}} = \overrightarrow {{n_\Delta }} = \left( {1;1} \right)\). Phương trình đường thẳng a là:
\(1\left( {x + 1} \right) + 1\left( {y - 0} \right) = 0 \Leftrightarrow x + y + 1 = 0\)
c) Ta có: \(\overrightarrow {{u_a}} = \overrightarrow {{n_\Delta }} = \left( {1;1} \right)\).Từ đó suy ra \(\overrightarrow {{n_b}} = \left( {1; - 1} \right)\). Phương trình đường thẳng b là:
\(1\left( {x - 0} \right) - 1\left( {y - 3} \right) = 0 \Leftrightarrow x - y + 3 = 0\)

bạn ơi tại sao khoảng cách bé nhất lại cho =0 z bạn

Đáp án: D
Khoảng cách từ điểm M(3;-4) đến đường thẳng d: 3x - 4y - 1 = 0 là:
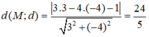

Do K là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}x_K=\frac{x_A+x_B}{2}=-2\\y_K=\frac{y_A+y_B}{2}=-1\end{matrix}\right.\) \(\Rightarrow K\left(-2;-1\right)\)
Áp dụng công thức khoảng cách:
\(d\left(K;d\right)=\frac{\left|-2.1-1.1+5\right|}{\sqrt{1^2+1^2}}=\sqrt{2}\)

a) Khoảng cách từ gốc tọa độ \(O\left( {0;0} \right)\) đến điểm \(M\left( {3;4} \right)\) trong mặt phẳng tọa độ Oxy là:
\(OM = \left| {\overrightarrow {OM} } \right| = \sqrt {{3^2} + {4^2}} = 5\)
b) Với hai điểm I(a; b) và M(x ; y) trong mặt phẳng toạ độ Oxy, ta có:\(IM = \sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2}} \)
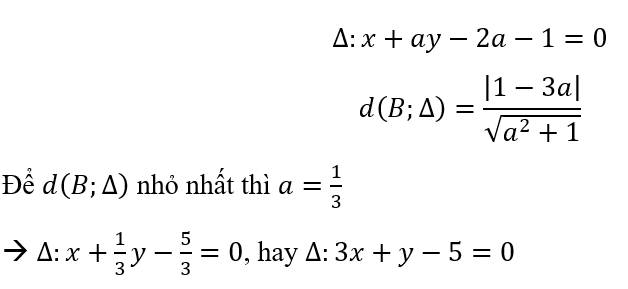
vecto BC=(3;3)=(1;1)
Phương trình BC là:
1(x-6)+1(y-2)=0
=>x+y-8=0
\(d\left(A;BC\right)=\dfrac{\left|1\cdot1+1\cdot4-8\right|}{\sqrt{1^2+1^2}}=\dfrac{3\sqrt{2}}{2}\)