Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi mặt phẳng là (P) dễ kí hiệu
\(d\left(M;\left(P\right)\right)=\frac{\left|-6+2+2-7\right|}{\sqrt{2^2+2^2+1}}=\frac{9}{3}=3\)
Áp dụng định lý Pitago:
\(R=\sqrt{3^2+4^2}=5\)
Phương trình mặt cầu:
\(\left(x+3\right)^2+\left(y-1\right)^2+\left(z-2\right)^2=25\)
\(\Leftrightarrow x^2+y^2+z^2+6x-2y-4z-11=0\)

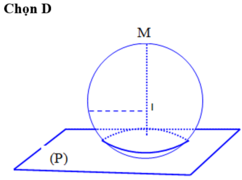
Mặt (S) cầu có tâm I (1;2;3), R=3.
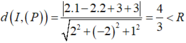 mặt phẳng cắt mặt cầu theo một đường tròn
mặt phẳng cắt mặt cầu theo một đường tròn
Gọi M (a;b;c) là điểm trên mặt cầu sao cho khoảng cách từ M đến (P) lớn nhất.
Khi M thuộc đường thẳng Δ vuông đi qua M và vuông góc với (P)
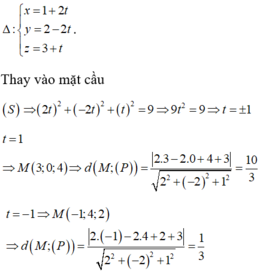
Vậy M (3;0;4) a + b + c = 7.

7.
\(\left(1+i\right)z=3z-i\Leftrightarrow\left(1+i-3\right)z=-i\)
\(\Leftrightarrow\left(i-2\right)z=-i\Rightarrow z=\frac{-i}{i-2}=-\frac{1}{5}+\frac{2}{5}i\)
Phần ảo là \(\frac{2}{5}\)
8.
\(\Leftrightarrow\left\{{}\begin{matrix}2x-1=2-x\\1-2y=3y+2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1\\y=-\frac{1}{5}\end{matrix}\right.\)
9.
\(\left|x-yi+2-i\right|=4\)
\(\Leftrightarrow\left(x+2\right)^2+\left(y+1\right)^2=16\)
Đường tròn tâm \(I\left(-2;-1\right)\) bán kính \(R=4\)
10.
Mặt cầu tâm \(I\left(1;2;2\right)\)
Khoảng cách: \(d\left(I;\alpha\right)=\frac{\left|1+2.2-2.2-4\right|}{\sqrt{1^2+2^2+\left(-2\right)^2}}=1\)
4.
Giao điểm d và (P) thỏa mãn:
\(1-t+2.2t-2\left(1+t\right)+2=0\Rightarrow t=-1\)
Thay vào pt d ta được tọa độ: \(\left(2;-2;0\right)\)
5.
Theo quy tắc nhân ta có \(3.4=12\) cách
6.
\(z=x+yi\Rightarrow5\left(x-yi\right)-\left(x+yi\right)\left(2-i\right)=2-6i\)
\(\Leftrightarrow3x-y-\left(7y-x\right)i=2-6i\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x-y=2\\-x+7y=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
\(\Rightarrow z=1+i\Rightarrow\left|z\right|=2\)
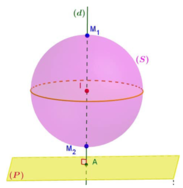



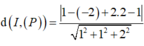






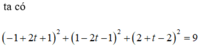
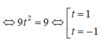
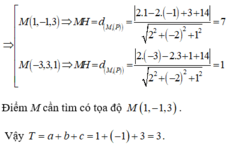
Mặt cầu tâm \(I\left(3;-2;1\right)\)
Mặt phẳng (P) nhận \(\left(1;2;2\right)\) là 1 vtpt
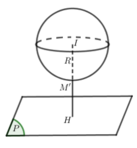
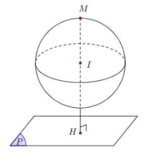
Gọi d là đường thẳng qua I và vuông góc (P) \(\Rightarrow\) M là giao điểm của d với mặt cầu (giao điểm nằm giữa I và H với H là giao của d và (P))
Phương trình tham số d: \(\left\{{}\begin{matrix}x=3+t\\y=-2+2t\\z=1+2t\end{matrix}\right.\)
H là giao d và (P) nên tọa độ thỏa mãn:
\(3+t+2\left(-2+2t\right)+2\left(1+2t\right)+11=0\Rightarrow t=-\frac{4}{3}\) \(\Rightarrow H\left(\frac{5}{3};-\frac{14}{3};-\frac{5}{3}\right)\)
M là giao d và (S) nên tọa độ thỏa mãn:
\(\left(3+t\right)^2+\left(-2+2t\right)^2+\left(1+2t\right)^2-6\left(3+t\right)+4\left(-2+2t\right)-2\left(1+2t\right)+5=0\)
\(\Leftrightarrow9t^2-9=0\Rightarrow\left[{}\begin{matrix}t=1\\t=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}M\left(4;0;3\right)\\M\left(2;-4;-1\right)\end{matrix}\right.\)
M nằm giữa I và H nên \(M\left(2;-4;-1\right)\) là điểm cần tìm