Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

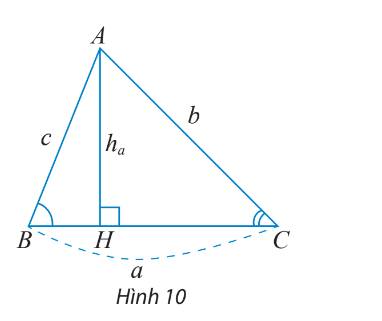
a) Diện tích S của tam giác ABC là: \(S = \frac{1}{2}a.{h_a}\)
b) Xét tam giác vuông AHC ta có: \(\sin C = \frac{{AH}}{{AC}} = \frac{{{h_a}}}{b}\)
\( \Rightarrow {h_a} = b.\sin C\)
c) Thay \({h_a} = b.\sin C\) vào công thức diện tích, ta được: \(S = \frac{1}{2}ab\sin C\)
d) Theo định lí sin ta có: \(\frac{c}{{\sin C}} = 2R \Rightarrow \sin C = \frac{c}{{2R}}\)
Thay vào công thức ở c) ta được: \(S = \frac{1}{2}ab\frac{c}{{2R}} = \frac{{abc}}{{4R}}.\)

Lớp A:
Trung bình cộng lớp A: \(\overline {{X_A}} = \frac{{148}}{{25}} = 5,92\)
Bảng tần số:
Điểm | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Số HS | 2 | 2 | 2 | 5 | 2 | 6 | 3 | 3 |
Do n=25 nên trung vị: số thứ 13
Do 2+2+2+5+2=13
=> Trung vị là 6.
Mốt là 7 do 7 có tần số là 6 (cao nhất)
Lớp B:
Trung bình cộng lớp B: \(\overline {{X_B}} = \frac{{157}}{{25}} = 6,28\)
Bảng tần số:
Điểm | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Số HS | 2 | 2 | 4 | 5 | 7 | 2 | 2 | 1 |
Do n=25 nên trung vị: số thứ 13
Do 2+2+4+5=13
=> Trung vị là 6.
Mốt là 7 do 7 có tần số là 7 (cao nhất)
Trừ số trung bình ra thì trung vị và mốt của cả hai mẫu số liệu đều như nhau
=> Hai phương pháp học tập hiệu quả như nhau.

Chọn A.
Do ![]() và
và ![]() là hai vectơ cùng hướng và đều khác vectơ
là hai vectơ cùng hướng và đều khác vectơ ![]() suy ra
suy ra ![]()
Do đó ![]()

a) Mệnh đề \(P \Rightarrow Q\) là: “Nếu \({a^2} < {b^2}\) thì \(0 < a < b\)”
b) Mệnh đề \(Q \Rightarrow P\) là: “Nếu \(0 < a < b\) thì \({a^2} < {b^2}\)”
c) Mệnh đề \(P \Rightarrow Q\) là: “Nếu \({a^2} < {b^2}\) thì \(0 < a < b\)” sai,
Chẳng hạn \(a = 2;\;b = -3\) ta có: \({2^2} < {( - 3)^2}\) nhưng không suy ra \(0<2<-3\).
Mệnh đề \(Q \Rightarrow P\) là: “Nếu \(0 < a < b\) thì \({a^2} < {b^2}\)” đúng.

a) Bảng 6:
| Lớp nhiệt độ (ºC) | Tần suất (%) | Giá trị đại diện |
| [15; 17] | 16,7 | 16 |
| [17; 19) | 43,3 | 18 |
| [19; 21) | 36,7 | 20 |
| [21; 23] | 3,3 | 22 |
| Cộng | 100 (%) |
Số trung bình cộng của bảng 6 là:
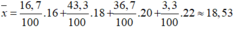
Số trung bình cộng của bảng 8 là:
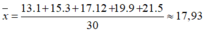
b) Nhiệt độ trung bình của thành phố Vinh trong tháng 12 cao hơn nhiệt độ trung bình trong tháng 2 khoảng 0,6ºC.

![]()
Từ đó suy ra:
- Bóng đèn ở lô A và bóng đèn ở lô B có tuổi thọ ngang nhau.
- Tuổi thọ của các bóng đèn ở lô A đồng đều hơn.
Đáp án: C

a) Kết quả trung bình của Cung thủ A là:
\(\frac{{8 + 9 + 10 + 7 + 6 + 10 + 6 + 7 + 9 + 8}}{{10}} = 8\)
Kết quả trung bình của Cung thủ A là:
\(\frac{{10 + 6 + 8 + 7 + 9 + 9 + 8 + 7 + 8 + 8}}{{10}} = 8\)
b)
+) Khoảng biến thiên số điểm của cung thủ A là: \(R = 10 - 6 = 4\)
Xét mẫu số liệu đã sắp xếp là:
\(\begin{array}{*{20}{c}}6&6&7&7&8&8&9&9&{10}&{10}\end{array}\)
Cỡ mẫu là \(n = 10\) là số chẵn nên giá trị tứ phân vị thứ hai là: \({Q_2} = 8.\)
Tứ phân vị thứ nhất là trung vị của mẫu:\(6,6,7,7,8\). Do đó \({Q_1} = 7.\)
Tứ phân vị thứ ba là trung vị của mẫu: \(8,9,9,10,10\). Do đó \({Q_3} = 9\)
Khoảng tứ phân vị của mẫu là: \({\Delta _Q} = 9 - 7 = 2\)
+) Khoảng biến thiên số điểm của cung thủ A là: \(R = 10 - 6 = 4\)
Xét mẫu số liệu đã sắp xếp là:
\(\begin{array}{*{20}{c}}6&7&7&8&8&8&8&9&9&{10}\end{array}\)
Cỡ mẫu là \(n = 10\) là số chẵn nên giá trị tứ phân vị thứ hai là: \({Q_2} = 8.\)
Tứ phân vị thứ nhất là trung vị của mẫu:\(6,6,7,7,8\). Do đó \({Q_1} = 7.\)
Tứ phân vị thứ ba là trung vị của mẫu: \(8,9,9,10,10\). Do đó \({Q_3} = 9\)
Khoảng tứ phân vị của mẫu là: \({\Delta _Q} = 9 - 7 = 2\)
=> Nếu so sánh khoảng chênh lệch và khoảng tứ phân vị thì không xác định được kết quả của cung thủ nào ổn định hơn.

Khối lượng thực của vật nằm trong khoảng:
(26,4 - 0,05; 26,4 - 0,05) kg
hay (26,35; 26,35) kg
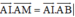 và
và 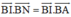
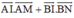 theo R.
theo R.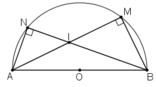
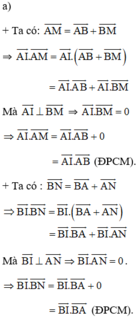

a) Hai bạn được chọn ở HĐ2a có vai trò như nhau, nói cách khác là không quan trọng thứ tự chọn.
Còn ở HĐ2b thì hai bạn có có vai trò khác nhau, nói cách khác là có xếp thứ tự lần lượt là lớp trưởng và lớp phó.
b) Số cách chọn 2 bạn (có xếp thứ tự) là 12 cách chọn.
Nhưng ở HĐ2a thì hai bạn có vai trò như nhau nên ta chia kết quả cho 2, tức là có 6 cách chọn (khi không xếp thứ tự)