Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

z_1+z_2=-m-1,z_1z_2=m^2+m-2/4, |z_1+z_2|<=|z_1|+|z_2|=/sqrt(10)->|m-1|<=\sqrt(10)->m=......
|z_1|+|z_2|>=2\sqrt(|z_1z_2|)= suy ra m=......
giao 2 cai lại r4a thôi

Δ=(a-2)^2-4(a^2-2a)
=-3a^2+4a+4
Để phương trình có hai nghiệm phân biệt thì -3a^2+4a+4<>0
=>a<>2 và a<>-2/3
|z1-z2|=|z1+z2|
=>(z1-z2)^2=(z1+z2)^2
=>z1z2=0
=>a^2-2a=0
=>a=0(nhận) hoặc a=2(loại)
=>Có 1 giá trị
Giải giúp mình bài này luôn với ạ
https://hoc24.vn/cau-hoi/1-trong-mat-phang-toa-do-oxy-cho-hai-diem-a02-b42-tim-diem-m-tren-doan-thang-ab-de-parabol-p-dinh-o-va-di-qua-diem-m-chia-tam-giac-vuong-oab-thanh-hai-phan-co-dien-tich-bang-nhau2-cho-h.7896187554129

\(\Delta'=m^2-8m+12\)
TH1: \(\Delta'< 0\Rightarrow\) phương trình có 2 nghiệm phức \(z_1;z_2\)
Do \(z_1=m-\sqrt[]{\Delta'};z_2=m+\sqrt{\Delta'}\Rightarrow z_1;z_2\) luôn luôn là 2 số phức liên hợp
\(\Rightarrow\left|z_1\right|=\left|z_2\right|\) luôn đúng khi \(m^2-8m+12< 0\)
\(\Rightarrow2< m< 6\Rightarrow m=\left\{3;4;5\right\}\)
TH2: \(\Delta'=0\Rightarrow m^2-8m+12=0\Rightarrow m=\left\{2;6\right\}\) pt có nghiệm kép (ktm)
TH3: \(\Delta'>0\Rightarrow\left[{}\begin{matrix}m>6\\m< 2\end{matrix}\right.\)
Pt có 2 nghiệm thực phân biệt, để \(\left|z_1\right|=\left|z_2\right|\Rightarrow\left[{}\begin{matrix}z_1=z_2\left(loại\right)\\z_1=-z_2\end{matrix}\right.\)
\(\Rightarrow z_1+z_2=0\Rightarrow2m=0\Rightarrow m=0\)
Vậy \(m=\left\{0;3;4;5\right\}\) có 4 giá trị nguyên của m

Đáp án A
Phương pháp.
Giả sử ![]() Giả phương trình ban đầu để tìm được nghiệm
z
1
,
z
2
Sử dụng giả thiết để đánh giá cho cho b. Đưa
Giả phương trình ban đầu để tìm được nghiệm
z
1
,
z
2
Sử dụng giả thiết để đánh giá cho cho b. Đưa ![]() về một hàm cho b và sử dụng ước lượng cho b ở phần trước để tìm giá trị nhỏ nhất của P.
về một hàm cho b và sử dụng ước lượng cho b ở phần trước để tìm giá trị nhỏ nhất của P.
Lời giải chi tiết.
Tính toán ta tìm được hai nghiệm 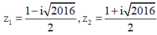
Giả sử ![]() . Từ
. Từ ![]() ta suy ra
ta suy ra
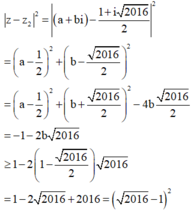
Áp dụng (1) ta nhận được
Do đó giá trị nhỏ nhất của ![]() là
2016
-
1
là
2016
-
1
Đạt được khi và chỉ khi ![]()

Đáp án D
Phương pháp
Biện luận để tìm trực tiếp nghiệm z 1 , z 2 . Sử dụng giả thiết để tìm ra giá trị m 0
Lời giải chi tiết.
Viết lại phương trình đã cho thành ![]()
Nếu m 0 = 9 ⇒ z = 3 Hay phương trình chỉ có một nghiệm. (Loại)
Nếu
m
0
<
9
thì phương trình đã cho có hai nghiệm thực ![]()

Nếu m 0 > 9 thì phương trình đã cho có hai nghiệm phức liên hợp là
![]()
Khi đó ![]()
Do đó m 0 > 9 thỏa mãn yêu cầu bài toán.
Do bài toán đòi hỏi
m
0
∈
(
0
;
20
)
nên ![]()
Vậy có 10 giá trị thỏa mãn.




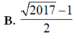
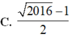
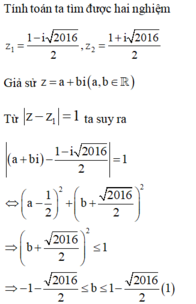

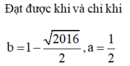
\(z^2-2\left(2m-1\right)z+m^2=0\)
Theo Vi - ét, ta có :
\(\left\{{}\begin{matrix}z_1+z_2=-\dfrac{b}{a}=2\left(2m-1\right)=4m-2\\z_1z_2=\dfrac{c}{a}=m^2\end{matrix}\right.\)
Ta có :
\(z^2_1+z_2^2=2\)
\(\Leftrightarrow\left(z_1+z_2\right)^2-2z_1z_2=2\)
\(\Leftrightarrow\left(4m-2\right)^2-2m^2-2=0\)
\(\Leftrightarrow16m^2-16m+4-2m^2-2=0\)
\(\Leftrightarrow14m^2-16m+2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=1\\m=\dfrac{1}{7}\end{matrix}\right.\)
Ta có phương trình bậc hai trên tập số phức:
z^2 - 2(2m-1)z + m^2 = 0
Theo định lý giá trị trung bình, nếu z1 và z2 là nghiệm của phương trình trên, thì ta có:
z1 + z2 = 2(2m-1) và z1z2 = m^2
Từ phương trình z1^2 + z2^2 = 2, ta suy ra:
(z1+z2)^2 - 2z1z2 = 4
Thay z1+z2 và z1z2 bằng các giá trị đã biết vào, ta được:
(2(2m-1))^2 - 2m^2 = 4
Đơn giản hóa biểu thức ta có:
m^2 - 4m + 1 = 0
Suy ra:
m = 2 + √3 hoặc m = 2 - √3
Vậy, để phương trình có hai nghiệm phân biệt thỏa mãn z1^2 + z2^2 = 2, ta cần phải có m = 2 + √3 hoặc m = 2 - √3.
Kết luận: Có hai giá trị của m để phương trình có hai nghiệm phân biệt thỏa mãn z1^2 + z2^2 = 2, đó là m = 2 + √3 hoặc m = 2 - √3.