Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C

Giai đoạn 1:
M1 chuyển động từ M đến O, sợi dây bị kéo căng =>
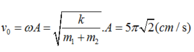
Giai đoạn 2:
M1 chuyển động từ O đến N, sợi dây chùng =>
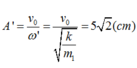
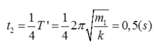
Giai đoạn 3:
M1 đi thêm từ N đến P, sợi dây chùng
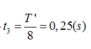
Giai đoạn 4:
M1 đi thêm từ P đến N, sợi dây chùng
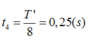
Giai đoạn 5:
M1 đi thêm từ N đến O, sợi dây chùng
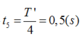
=> trong 1 chu kỳ, khoảng thời gian dây trùng là :0,5+0,25+0,25+0,5=1,5(s)

Phương pháp: Sử dụng phương pháp động lực học và phương pháp bảo toàn năng lượng.
Cách giải:
Hai vật chuyển động đến vị trí vận tốc cực đại, vị trí đó là

Khi hai vật tách nhau ra, vật 1 tiếp tục dao động, vật 2 chuyển động chậm dần rồi dừng lại.
Gia tốc chuyển động của vật 2 là:

Đáp án C

Hướng dẫn:
+ Vật m 2 sẽ rời khỏi m 2 khi hai vật này đi qua vị trí cân bằng tạm lần đầu tiên
→ Tốc độ của vật m 2 tại vị trí này
v 0 = ω X 0 − x 0 = k m 1 + m 2 X 0 − μ m 1 + m 2 g k = 50 0 , 1 + 0 , 4 0 , 1 − 0 , 05 0 , 1 + 0 , 4 .10 50 = 0 , 95
+ Quãng đường m 2 đi được từ khi rời vật m 1 đến khi dừng lại 1 2 m 2 v 0 2 = μ m 2 g S → S = v 0 2 2 μ g = 0 , 9025 m
→ Vậy tổng thời gian từ khi thả vật m 2 đến khi m 2 dừng lại là t = T 4 + 2 S μ g = 2 , 056 s
Đáp án C

Hướng dẫn:
Giai đoạn 1: Hai vật dao động điều hòa với biên độ A = 8 cm quanh vị trí cân bằng O từ biên về vị trí cân bằng.
+ Tần số góc dao động của hệ ω = k m 1 + m 2 = k 2 m rad/s.
→ Khi hệ hai vật đến O, ta có v = v m a x = ω A = 8 ω c m / s .
Giai đoạn 1: Vật m1 dao động điều hòa quanh vị trí cân bằng O, vật m2 chuyển động thẳng đều ra xa với tốc độ v 2 = v m a x .
+ Tần số góc của con lắc sau khi vật m 2 tách ra khỏi m 1 ω ' = k m 1 = k m = 2 ω rad/s → T ' = 2 π 2 ω = 2 π ω s.
Tại vị trí vật m 2 tách khỏi vật m 1 , ta có x′ = 0, v ′ = v m a x .
→ Biên độ dao động mới của m 1 là A 1 = v m a x ω ' = 8 ω ω ' = 4 2 cm.
+ Lò xo giãn cực đại lần đầu tiên kể từ thời điểm hai vật tách nhau ứng với Δt = 0,25T s.
→ Khoảng cách giữa hai vật lúc đó là Δ x = x 2 − x 1 = v m a x T ' 4 − A 1 = 8 ω 2 π 4 ω − 4 2 = 3 , 22 cm.
Đáp án D




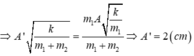
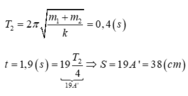
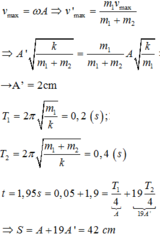

Va chạm đàn hồi không thi đâu bạn, không nên quan tâm về nó.
Gọi v1, v2 là vận tốc của vật m1, m2 sau va chạm, áp dụng CT tính vận tốc trong va chạm đàn hồi ta có:
\(\Rightarrow v_2 = \frac{2m_1.v_{max}}{m_1 + m_2} = \frac{2.0,1.0,1. \sqrt{\frac{100}{0,1}}}{0,1 + 0,5} = \frac{10\sqrt{10}}{30} = \frac{\sqrt{10}}{3}\) (m/s)
và
\( v_1 = \frac{m_1.v_{max} - v_2.m_2}{m_1} = A\omega - \frac{\sqrt{10}}{3}.5 = -\frac{2\sqrt{10}}{3}\) (m/s), \(v_1 <0\) nên vật m1 chuyển động theo chiều ngược lại.
Biên độ mới của vật m1 là A mới = \(\frac{v_1}{\omega } = \frac{\frac{2\sqrt{10}}{3}}{10\sqrt{10}} = \frac{2}{30} \)(m) = \(\dfrac{20}{3}\) (cm)
Sau T/4 thì 2 vật mới chuyển động cùng chiều ⇒ Quãng đường S m2 đi được là \(S = v_2.T/4 = \frac{\sqrt{10}}{3}.\frac{T}{4} = \frac{\sqrt{10}}{60}\) (m)
Khoảng cách = A mới + S = \(\frac{2}{30} + \frac{\sqrt{10}}{60} = 11,94\) (cm)
Còn khoảng cách gần nhất được tính như sau:
\(x_{m1} = A. cos(10 \pi t - \pi) = \frac{2}{30} cos(10 \pi t - \pi)\)
\(x_{m2} = v_2t = \frac{\sqrt{30}}{3}t\)
⇒ Khoảng cách = \(\left | x_{M2} - x_{M1} \right | = \frac{\sqrt{10}}{3}t - \frac{22}{30}cos(100 \pi t - \pi)\)
Khi vật m1 tới vị trí có khoảng cách gần m2 nhất thì tốc độ của m1 bằng tốc độ m2,
\(\Rightarrow x = \frac{A\sqrt{3}}{2}\) ⇒ sau thời gian là T/2 + T/6 ⇒quãng đường vật m2 đi được là
\(s_2 = v_2.t = \frac{\sqrt{10}}{3} . \frac{2T}{3} = 14,05\) cm.
⇒ Khoảng cách = \(14,05 - x = 14,05 - \frac{10}{\sqrt{3}} = 8,2 \) cm
⇒ Chọn đáp án C.