Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Hướng dẫn:
+ Vật m 2 sẽ rời khỏi m 2 khi hai vật này đi qua vị trí cân bằng tạm lần đầu tiên
→ Tốc độ của vật m 2 tại vị trí này
v 0 = ω X 0 − x 0 = k m 1 + m 2 X 0 − μ m 1 + m 2 g k = 50 0 , 1 + 0 , 4 0 , 1 − 0 , 05 0 , 1 + 0 , 4 .10 50 = 0 , 95
+ Quãng đường m 2 đi được từ khi rời vật m 1 đến khi dừng lại 1 2 m 2 v 0 2 = μ m 2 g S → S = v 0 2 2 μ g = 0 , 9025 m
→ Vậy tổng thời gian từ khi thả vật m 2 đến khi m 2 dừng lại là t = T 4 + 2 S μ g = 2 , 056 s
Đáp án C
Phương pháp: Sử dụng phương pháp động lực học và phương pháp bảo toàn năng lượng.
Cách giải:
Hai vật chuyển động đến vị trí vận tốc cực đại, vị trí đó là
Khi hai vật tách nhau ra, vật 1 tiếp tục dao động, vật 2 chuyển động chậm dần rồi dừng lại.
Gia tốc chuyển động của vật 2 là:
Đáp án C
Khoảng thời gian giữa 2 lần liên tiếp động ăng bằng thế năng là T/4
\(\Rightarrow \dfrac{T}{4}=\dfrac{\pi}{40}\)
\(\Rightarrow T = \dfrac{\pi}{10}\)
\(\Rightarrow \omega=\dfrac{2\pi}{T}=20(rad/s)\)
Biên độ dao động: \(A=\dfrac{v_{max}}{\omega}=\dfrac{100}{20}=5(cm)\)
Ban đầu, vật qua VTCB theo chiều dương trục toạ độ \(\Rightarrow \varphi=-\dfrac{\pi}{2}\)
Vậy PT dao động là: \(x=5\cos(20.t-\dfrac{\pi}{2})(cm)\)
Đáp án B
Nên nhớ các công thức trong dao động tắt dần:
Quãng đường vật đi được đến khi dừng hẳn: s = k A 2 2 μ m g
Thay số vào ta được: s = 10 . 0 , 07 2 2 . 0 , 1 . 0 , 1 . 10 = 0 , 245 m = 24 , 5 c m
Giải thích: Đáp án B
Phương pháp: Vận tốc ở VTCB: v = ωA
Cách giải:
Khi về đến VTCB thì cả hai vật có vận tốc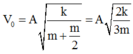 
Sau đó vật m sẽ dao động với chu kỳ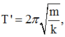 
và biên độ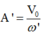 
Vật M sẽ tiếp tục chuyển động thẳng đều với vận tốc V0
Ở thời điểm lò xo có chiều dài cực đại lần đầu tiên m đến vị trí biên A’, còn M đi được quãng đường là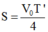 
=> Khoảng cách giữa hai vật m và M là:d = S - A’=4,19cm.
Ta có: \(\begin{cases}\Delta l_1=l_1-l_0=\frac{g}{\omega^2_1}\\\Delta l_2=l_2-l_0=\frac{g}{\omega^2_2}\end{cases}\)\(\Rightarrow\frac{\omega^2_2}{\omega^2_1}=\frac{21-l_0}{21,5-l_0}=\frac{1}{1,5}\)\(\Rightarrow l_0=20\left(cm\right)\)
\(\Rightarrow\Delta l_1=0,01\left(m\right)=\frac{g}{\omega^2_1}\Rightarrow\omega_1=10\pi\left(rad/s\right)\)
KQ = 3,2 cm
Đáp án C
+ Vật bắt đầu giảm tốc tại vị trí: x 0 = μ m g 2 k = 0,02m
Vị trí này được coi vị trí cân bằng ảo trong dao động tắt dần.
+ Năng lượng mất đi để chống lại lực ma sát. Vì vậy cơ năng mất tính bởi A = μ m g s = μ m g ( A - x 0 ) = 7,2 mJ
Hướng dẫn: Chọn đáp án C
Vì số liệu ở các phương án lệch xa nhau nên ta có thể giải theo cả hai cách
Chú ý: Để tìm chính xác tổng quãng được đi được ta dựa vào định lí “Độ giảm cơ năng đúng bằng công của lực ma sát”
