Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\left\{{}\begin{matrix}p+e+n=60\\p=e\\p+e-n=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2n=40\\p=e\\p+e-n=20\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}p=e=20\\n=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}p=e=z=20\\n=20\end{matrix}\right.\)
\(\Rightarrow A=z+n=20+20=40\left(u\right)\)
\(KHNT:^{40}_{20}Ca\)
\(\left\{{}\begin{matrix}2Z+N=60\\2Z-n=20\end{matrix}\right.\)
\(\Rightarrow\)\(\left\{{}\begin{matrix}Z=20\\N=20\end{matrix}\right.\)
\(\Rightarrow\)\(A=Z+N=20+20=40u\)
Kí hiệu nguyên tử \(^{40}_{20}X\)

Z = số proton = số electron. N = số nơtron
Theo đề bài ta có : 2Z + N = 34
Ta biết rằng trong hạt nhân, số nơtron bao giờ cũng bằng hoặc lớn hơn số proton (trừ trường hợp duy nhất là hiđro có Z = 1).
N > Z. Vì vậy ta có : 3Z < 34, do đó Z < 34/3 = 11,3 (1)
Cũng vì N ≥ Z nên theo điều kiện của đề bài Z < 20, do đó :
N/Z ≤ 1,2 → N ≤ 1,2Z
Từ đó ta có : 2Z + N < 2Z + 1,2Z
34 < 3,2 => Z > 34/3,2 = 10,6 (2)
Tổ hợp (1) và (2) ta có : 10,6 < Z < 11,3 mà Z nguyên. Vậy Z = 11. Đó là nguyên tố natri có 11 proton, 11 electron, 12 nơtron.
Số khối của nguyên tử : A = Z + N = 23 => NTK là 23

ta co p+e+n=93 mà p=e=z => 2z+n=93
2z-n=23 ( vì số hạt mang điện nhiều hơn số hạt ko mang điện là 23)
tu 2 pt trên ta có z =29,,n=35
=> số hiệu nguyên tử của B = Z = 29
cấu hình electron
\(1s^22s^22p^63s^23p^64s^23d^9\)
đối với các dạng bài này , bạn cần nhớ kiến thức như sau :
Tổng số hạt trong nguyên tử = 2p + n ( gồm có 3 loại hạt : n , p, e trong đó p=e)
số hạt mang điện là 2p
số hạt không mang điện là n
số hiệu nguyên tử là Z= p = e = số thứ tự nhóm .
Sau khi xác định được p ,, tức là cũng xác định được e thì
cấu hình viết theo dãy trật tự các mức năng lượng
1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d10.......
Các nguyên tử có 1, 2, 3e ở lớp ngoài cùng là các nguyên tử kim loại, trừ H, He và B.Các nguyên tử có 5, 6, 7e ở lớp ngoài cùng thường là các nguyên tố phi kim. Các nguyên tử có 4e ở lớp ngoài cùng có thể là nguyên tử kim loại hoặc phi kim
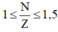
Ta có: \(1\le\dfrac{N}{Z}\le1,5\)
\(\Rightarrow Z\le N\le1,5Z\)
\(\Rightarrow3Z\le2Z+N\le3,5Z\)
Vậy ta có : \(3Z\le24\le3,5Z\)
=> \(6,86\le Z\le8\)
=>\(\left[{}\begin{matrix}Z=7\left(N\right)\\Z=8\left(O\right)\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}N=10\\N=8\end{matrix}\right.\)
Mà theo đề bài : \(1\le\dfrac{N}{Z}\le1,5\)
=> Chỉ có O thỏa mãn
=> Z là O , số P= số E =8 , N=8
b) Cấu hình E: 1s22s22p4