K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SG
1
DD
1
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 1 2021
\(S_n=3^n-1\)
\(S=2011\left(u_1+...+u_{2010}\right)-\left(u_1+...+u_{2009}\right)-\left(u_1+...+u_{2008}\right)-...-u_1\)
\(=2011S_{2010}-\left(S_{2009}+S_{2008}+...+S_1\right)\)
\(=2011\left(3^{2010}-1\right)-\left(3^{2009}-1+3^{2008}-1+...+3^1-1\right)\)
\(=2011\left(3^{2010}-1\right)-\left(3.\dfrac{3^{2009}-1}{3-1}-2009\right)\)
\(=...\)
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) \({u_2} = {u_1} + d\)
\({u_3} = {u_1} + 2d\)
…
\({u_{n - 1}} = {u_1} + \left( {n - 2} \right)d\)
\({u_n} = {u_1} + \left( {n - 1} \right)d\)
\({S_n} = {u_1} + {u_1} + 2d + \ldots + {u_1} + \left( {n - 2} \right)d + {u_1} + \left( {n - 1} \right)d\)
b) \({S_n} = {u_n} + {u_{n - 1}} + \ldots + {u_2} + {u_1} = {u_1} + \left( {n - 1} \right)d + {u_1} + \left( {n - 2} \right)d + \ldots + {u_1} + d + {u_1}\)
c) \(2{S_n} = \left( {{u_1} + {u_1} + d + \ldots + {u_1} + \left( {n - 1} \right)d} \right) + \left( {{u_1} + \left( {n - 1} \right)d + {u_1} + \left( {n - 2} \right)d + \ldots + {u_1}} \right)\).
\( \Rightarrow 2{S_n} = n.\left( {2{u_1} + \left( {n - 1} \right)d} \right)\)
\( \Rightarrow {S_n} = \frac{n}{2}\left( {2{u_1} + \left( {n - 1} \right)d} \right)\)
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) \({u_2} = {u_1}.q\)
\({u_3} = {u_1}.{q^2}\)
…
\({u_{n - 1}} = {u_1}.{q^{n - 2}}\)
\({u_n} = {u_1}.{q^{n - 1}}\)
\({S_n} = {u_1} + {u_1}q + \ldots + {u_1}{q^{n - 2}} + {u_1}{q^{n - 1}}\)
b) \(q{S_n} = q{u_1} + {u_1}{q^2} + \ldots + {u_1}{q^{n - 1}} + {u_1}{q^n}\)
c) \({S_n} - q{S_n} = \left( {{u_1} + {u_1}q + \ldots + {u_1}{q^{n - 2}} + {u_1}{q^{n - 1}}} \right) - (q{u_1} + {u_1}{q^2} + \ldots + {u_1}{q^{n - 1}} + {u_1}{q^n})\).
\(\begin{array}{l} \Leftrightarrow \left( {1 - q} \right){S_n} = {u_1} - {u_1}{q^n} = {u_1}\left( {1 - {q^n}} \right)\\ \Rightarrow {S_n} = \frac{{{u_1}\left( {1 - {q^n}} \right)}}{{1 - q}}\end{array}\)
MH
9 tháng 4 2017
a) Ta có:
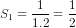
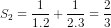
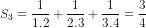
b) Từ câu a) ta dự đoán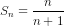 
(1), với mọi n ε N* .
Ta sẽ chứng minh đẳng thức (1) bằng phương pháp quy nạp
Khi n = 1, vế trái là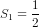 
, vế phải bằng 
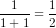. Vậy đẳng thức (1) đúng.
Giả sử đẳng thức (1) đúng với n = ≥ 1, tức là
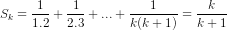
Ta phải chứng minh nó cũng đúng khi n = k + 1, nh=ghĩa là phải chứng minh
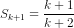
Ta có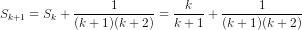 
= 
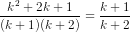
tức là đẳng thức (1) cũng đúng với n = k + 1.
Vậy điều cần chứng minh đúng với mọi n.
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
Nếu cấp số nhân có công bội q = 1 thì cấp số nhân là \(u_1, u_1, ..., u_1,...\) Khi đó
\({S_n} = u_1 + u_1 + ... + u_1 = n . u_1\) (tổng của n số hạng u_1).
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Ta có:
\({S_n}.q = \left( {{u_1} + {u_1}q + {u_1}{q^2} + ... + {u_1}{q^{n - 1}}} \right).q = {u_1}\left( {1 + q + {q^2} + ... + {q^{n - 1}}} \right).q = {u_1}\left( {q + {q^2} + {q^3} + ... + {q^n}} \right)\)
\(\begin{array}{l}{S_n} - {S_n}.q = {u_1} + {u_1}q + {u_1}{q^2} + ... + {u_1}{q^{n - 1}} - {u_1}\left( {q + {q^2} + {q^3} + ... + {q^n}} \right)\\ = {u_1}\left( {1 + q + {q^2} + ... + {q^{n - 1}}} \right) - {u_1}\left( {q + {q^2} + {q^3} + ... + {q^n}} \right)\\ = {u_1}\left( {1 + q + {q^2} + ... + {q^{n - 1}} - \left( {q + {q^2} + {q^3} + ... + {q^n}} \right)} \right)\\ = {u_1}\left( {1 - {q^n}} \right)\end{array}\)
b) Ta có: \({S_n} - {S_n}.q = {u_1}\left( {1 - {q^n}} \right) \Leftrightarrow {S_n}\left( {1 - q} \right) = {u_1}\left( {1 - {q^n}} \right) \Leftrightarrow {S_n} = \frac{{{u_1}\left( {1 - {q^n}} \right)}}{{\left( {1 - q} \right)}}\)
Ta có : \(S=3\left(1+11+111+...+11...1\right)\) (n chữ số 1)
\(=3\left(\frac{10-1}{9}+\frac{10^2-1}{9}+....\frac{10^n-1}{9}\right)=\frac{3}{9}\left(10+10^2+....+10^n-n\right)\)
\(=\frac{1}{3}\left(10.\frac{10^n-1}{10-1}-n\right)=\frac{1}{27}\left(10^{n+1}-10-9n\right)\)