Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(B=x^{17}-12.x^{16}+12.x^{15}-12.x^{14}+...-12.x^2+12x-1\)
\(=11^{17}-\left(11+1\right)11^{16}+\left(11+1\right)11^{15}-\left(11+1\right)11^{14}+...-\left(11+1\right)11^2+\left(11+1\right)11-1\)
\(=11^{17}-11^{17}-11^{16}+11^{16}+11^{15}-11^{15}-11^{14}+...-11^3-11^2+11^2+11-1\)
\(=11-1=10\)
Vậy B = 10

\(B=x^5-15x^4+16x^3-29x^2+13x\)
\(=x^5-14x^4-x^4+14x^3+2x^3-28x^2-x^2+14x-x+14-14\)
\(=x^4\left(x-14\right)-x^3\left(x-14\right)+2x^2\left(x-14\right)-x\left(x-14\right)-\left(x-14\right)-14\)
\(=\left(x^4-x^3+2x^2-x-1\right)\left(x-14\right)-14\)
Thay x = 14 => B = -14
Vậy...
phần còn lại tách ra làm tương tự nhé

a=x4-2223x3+2223x2-2223x+2223
=x3(x-2223)+x(x-2223)+2222x2+2003(*)
thay x=2222,ta co:
(*)<=>-22223-2222+22223+2223=1
dung thi chon nha

Nếu \(x=9\Rightarrow10=x+1\)
Thay \(10=x+1\) vào A , ta được :
\(A=x^{14}-\left(x+1\right)x^{13}+\left(x+1\right)x^{12}-\left(x+1\right)x^{11}+...+\left(x+1\right)x^2-\left(x+1\right)x+x+1\)
\(=x^{14}-x^{14}-x^{13}+x^{13}+x^{12}-x^{12}-x^{11}+...+x^3+x^2-x^2-x+x+1\)
\(=1\)
Vậy \(A=1\) tại \(x=9\)

x=7
=>x+1=8
=> A= x^15 - 8x^14 + 8x^13 - 8x^12 +....- 8x^2 + 8x - 5
=x15-(x+1)x14+(x+1)x13-(x+1)x12+...-(x+1)x2+(x+1)x-5
=x15-x15-x14+x14+x13-x13-x12+...-x3-x2+x2+x-5
=x-5
=>A=7-5=2
Vậy A=2 khi x=7
\(B=x^{15}-8x^{14}+8x^{13}-8x^{12}+...+8x-5\)
\(=x^{15}-\left(x+1\right)x^{14}+\left(x+1\right)x^{13}-\left(x+1\right)x^{12}+...+\left(x+1\right)x-x+2\)
\(=x^{15}-x^{15}-x^{14}+x^{14}+x^{13}-x^{13}-x^{12}+...+x^2+x-x+2\)
\(=2\)
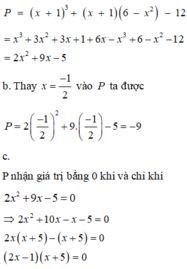
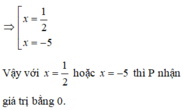
x=11 suy ra 12=x+1 thay vào A ta có:
A=x^17- (x+1)x^16 + (x+1)x^15 - (x+1)x^14 + .....- (x+1)x^2+(x+1)x -1
= x^17 - x^17 -x^16 + x^16 + x^15 - x^15 - x^14 +.....- x^3 -x^2 + x^2 +x -1
= x-1= 11-1=10