BH
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NP
0
Q
2
AH
Akai Haruma
Giáo viên
24 tháng 8 2021
Lời giải:
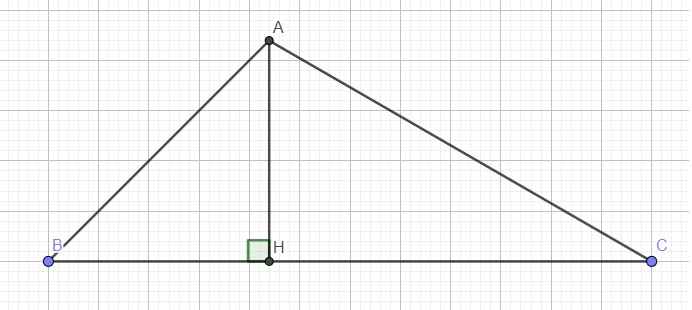
Từ $A$ kẻ $AH\perp BC$.
Xét tam giác $ABH$: $\frac{AH}{BH}=\tan B$
$\Rightarrow BH=\frac{AH}{\tan B}=\frac{AH}{\tan 50^0}$
Xét tam giác $ACH$: $\frac{AH}{CH}=\tan C$
$\Rightarrow CH=\frac{AH}{\tan C}=\frac{AH}{\tan 30^0}$
Do đó:
$BC=BH+CH=AH(\frac{1}{\tan 50^0}+\frac{1}{\tan 30^0})$
$10=AH(\frac{1}{\tan 50^0}+\frac{1}{\tan 30^0})$
$AH=3,89$ (cm)
$S_{ABC}=\frac{AH.BC}{2}=\frac{3,89.10}{2}=19,45$ (cm vuông)
MN
1
HL
2
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 7 2021
Kẻ đường cao AH
Trong tam giác vuông ABH:
\(cotB=\dfrac{BH}{AH}\Rightarrow BH=AH.cotB\)
Trong tam giác vuông ACH:
\(cotC=\dfrac{CH}{AH}\Rightarrow CH=AH.cotC\)
\(\Rightarrow BH+CH=AH.cotB+AH.cotC\)
\(\Leftrightarrow BC=AH\left(cotB+cotC\right)\)
\(\Leftrightarrow AH=\dfrac{BC}{cotB+cotC}\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.\dfrac{BC^2}{cotB+cotC}=\dfrac{1}{2}.\dfrac{6^2}{cot45^0+cot30^0}\approx11,4\left(cm^2\right)\)
:>>>>>>>>>