MT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
2
28 tháng 8 2019
\(x=\frac{4}{1+4}=\frac{4}{5}=0,8\) \(z=\frac{4}{1+4}=\frac{4}{5}=0,8\)
\(y=\frac{4}{1+4}=\frac{4}{5}=0,8\)
22 tháng 1 2019
Ta có:
\(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0\)
\(\Leftrightarrow\frac{yz+zx+xy}{xyz}=0\) (Quy đồng)
\(\Rightarrow yz+zx+xy=0\)
Vì:
\(\left(x^2y^2+y^2z^2+z^2x^2\right)^2=0\)
\(2\left(x^4y^{ }^4+y^4z^4+z^4x^4\right)=0\)
Nên.....(tự kết luận nha)
23 tháng 1 2019
giải chi tiết ( vì sao ) đoạn dưới đây = 0 hộ mk vs :
vì \(\left(x^2y^2+y^2z^2+z^2x^2\right)^2=0\)
\(2\left(x^4y^4+y^4z^4+z^4x^4\right)=0\)
18 tháng 3 2018
Ta có 1/x+1/y+1/z=0
=>1/x+1/y=-1/z
=>(1/x+1/y)^3= (-1/z)^3
=>1/x^3+1/y^3+3.1/x.1/y.(1/x+1/y) =-1/z^3
=>1/x^3+1/y^3+1/z^3= -3.1/x.1/y.(1/x+1/y) =3/(xyz) (vì 1/x+1/y=-1/z)
Mặt khác: 1/x+1/y+1/z=0
=>(xy+yz+zx)/(xyz)=0
=>xy+yz+zx=0
A=yz/x^2 +2yz + xz/y^2+ 2xz + xy/z^2+ 2 xy
=xyz/x^3+xyz/y^3+xyz/z^3 +2(xy+yz+zx) (vì x,y,z khác 0)
=xyz(1/x^3+1/y^3+1/z^3) (vì xy+yz+zx=0)
=xyz.3/(xyz) (vì 1/x^3+1/y^3+1/z^3=3/(xyz) )
=3
Vậy A=3.
10 tháng 2 2022
a: x-y-z=0
=>x=y+z; y=x-z; z=x-y
\(K=\dfrac{x-z}{x}\cdot\dfrac{y-x}{y}\cdot\dfrac{z+y}{z}=\dfrac{y\cdot\left(-z\right)\cdot x}{xyz}=-1\)
b: Tham khảo:
22 tháng 2 2022
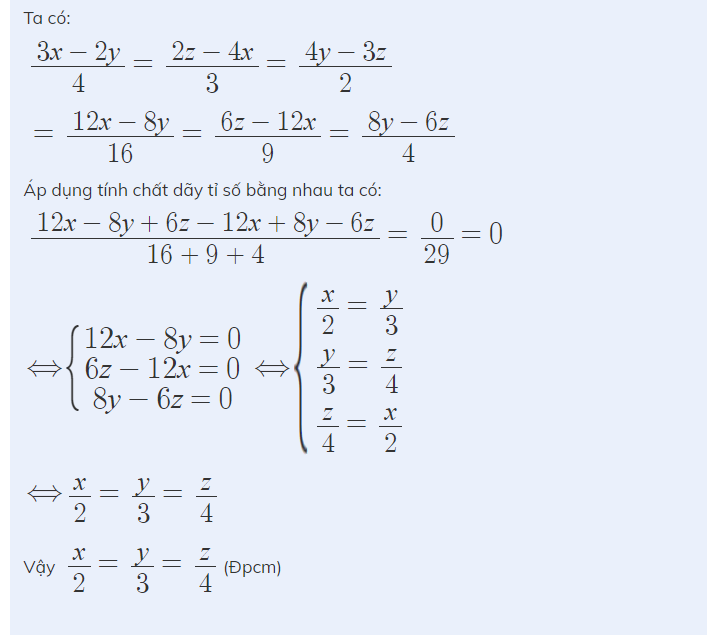
Bài 1:
\(=\dfrac{x-2+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}-1}=\dfrac{\sqrt{x}+1}{\sqrt{x}}\)